
Главная
Рефераты по зарубежной литературе
Рефераты по логике
Рефераты по маркетингу
Рефераты по международному публичному праву
Рефераты по международному частному праву
Рефераты по международным отношениям
Рефераты по культуре и искусству
Рефераты по менеджменту
Рефераты по металлургии
Рефераты по муниципальному праву
Рефераты по налогообложению
Рефераты по оккультизму и уфологии
Рефераты по педагогике
Рефераты по политологии
Рефераты по праву
Биографии
Рефераты по предпринимательству
Рефераты по психологии
Рефераты по радиоэлектронике
Рефераты по риторике
Рефераты по социологии
Рефераты по статистике
Рефераты по страхованию
Рефераты по строительству
Рефераты по схемотехнике
Рефераты по таможенной системе
Сочинения по литературе и русскому языку
Рефераты по теории государства и права
Рефераты по теории организации
Рефераты по теплотехнике
Рефераты по технологии
Рефераты по товароведению
Рефераты по транспорту
Рефераты по трудовому праву
Рефераты по туризму
Рефераты по уголовному праву и процессу
Рефераты по управлению
Дипломная работа: Проектирование агрегатного цеха пассажирского автотранспортного предприятия
Дипломная работа: Проектирование агрегатного цеха пассажирского автотранспортного предприятия
1. ТЕХНОЛОГИЧЕСКОЕ ПРОЕКТИРОВАНИЕ АГРЕГАТНОГО ЦЕХА ПАССАЖИРСКОГО АТП
1.1 Краткая характеристика проектируемого объекта
Целью отраслевой части дипломной работы является технологическое проектирование агрегатного цеха пассажирского автотранспортного предприятия (ПАТП), расположенного на окраине города. Автобусный парк включает: 6% условно – «новых» автобусов со средним пробегом с начала эксплуатации 75000 км, 54% условно – «старых» автобусов со средним пробегом с начала эксплуатации 315000 км, 40% после капитального ремонта автобуса со средним пробегом с начала эксплуатации 450000 км.
ПАТП выполняет пассажирские перевозки по дорогам 2 категории в условиях умеренного климата. Автобусы работают 365 дней в году по 2 смены (16 часов в сутки) при этом среднесуточный пробег составляет 260 км.
Капитальный ремонт автобусов проводится в авторемонтных мастерских (АРМ), расположенных на расстоянии 740 км от ПАТП. Доставка в АРМ осуществляется своим ходом со среднесуточным пробегом 370 км.
Для выполнения технических обслуживаний, диагностики и текущих ремонтов служат зоны и цеха, оборудованные специальным технологическим оборудованием, расположенные в главном производственном корпусе.
1.2 Расчетно-технологическая часть
1.2.1 Расчет годовой производственной программы ПАТП по ТО и ТР
В связи с тем, что парк «разновозрастной», находим численность автобусов в группах разного технического состояния.
Число автобусов не выполнивших норму пробега до первого капитального ремонта (условно – «новые») определяем по формуле (1)
ун =![]() , (1)
, (1)
где Аи – инвентарное число автобусов в парке, ед.;
Дун – процентное содержание условно – «новых» автобусов;
Аун = ![]() .
.
Число автобусов выполнивших норму пробега до капитального ремонта, но находящихся в эксплуатации (условно – «старые») определяем по формуле (2)
Аус =![]() , (2)
, (2)
где Дус – процентное содержание условно – «старых» автобусов;
Аус = ![]() .
.
Число автобусов после капитального ремонта (старых) определяем по формуле (3)
Ас =![]() , (3)
, (3)
где Дс – процентное содержание автобусов после капитального ремонта (старых);
Ас = ![]() .
.
Определяем средневзвешенную величину пробега автобусов по формуле (4)
![]() , (4)
, (4)
где Lц – цикловой пробег автобусов, (пробег с начала эксплуатации нового автобуса до его капитального ремонта), км.;
L'ц – цикловой пробег автобусов после капитального ремонта, принимаем
L'ц = Lц∙0,8;
L'ц = 360000∙0,8=288000;
Lц.ср.=![]() .
.
Находим усредненный корректированный цикловой пробег автобусов по формуле (5)
![]() , (5)
, (5)
где К1 – коэффициент корректирования пробега до КР в зависимости от условий эксплуатации, принимаем К1 = 0,9;
К2 – коэффициент корректирования пробега до КР в зависимости от модификации подвижного состава (ПС) и организации его работы, принимаем К2 = 1,0;
К3 – коэффициент корректирования пробега до КР в зависимости от природно-климатических условий, принимаем К3 = 1,0;
![]()
![]() .
.
Находим корректированный пробег между ТО-1 по формуле (6)
![]() , (6)
, (6)
где L1-нормативный пробег между ТО-1, принимаем L1= 4000 км.;
К1 – коэффициент корректирования периодичности ТО в зависимости от условий эксплуатации, принимаем К1 = 0,9;
К3 – коэффициент корректирования периодичности ТО в зависимости от природно-климатических условий, принимаем К3 = 1,0;
![]()
![]() .
.
Находим корректированный пробег между ТО-2 по формуле (7)
![]() , (7)
, (7)
где L2-нормативный пробег между ТО-2, принимаем L2= 16000 км.;
![]()
![]() .
.
Находим пробег между ЕО:
Lео = lcc= 260 км
Результаты вычислений сводим в таблицу 3
Таблица 3 - Периодичность ТО и цикловой пробег автобусов
| Вид пробега | Обозначение | Пробег, км | |||
| нормативный | откорректи-рованный | уточненный по кратности | принятый для дальнейших расчетов | ||
| Среднесуточный | lcc | 260 | - | - | 260 |
| До ТО-1 |
L1 |
4000 | 3600 | 260∙14 | 3640 |
| До ТО-2 |
L2 |
16000 | 14400 | 3640∙4 | 14560 |
| До КР |
Lц.ср. Lкц.ср. (Lкц.ср)′; Lц.р. |
360000 | 298080 | 14560∙21 | 305760 |
Определение количество ТО и Р за цикл (на 1 автобус)
Количество КР определяем по формуле (8)
![]() , (8)
, (8)
![]()
![]() .
.
Количество ТО-2 определяем по формуле (9)
![]() , (9)
, (9)
![]()
![]() .
.
Количество ТО-1 определяем по формуле (10)
![]() , (10)
, (10)
![]()
![]() .
.
Количество ЕО определяем по формуле (11)
![]() , (11)
, (11)
![]()
![]() .
.
Примечание: Neo.ц. численно совпадает с количеством дней эксплуатации автобусов за цикл (Дэ.ц.).
Определяем коэффициент технической готовности автобусов по формуле (12)
![]() ; (12)
; (12)
где Дэ.ц. – число дней эксплуатации автобуса за цикл определяем по формуле (13);
![]() ; (13)
; (13)
![]()
![]() ;
;
Дпр.ц. – число дней простоя автобуса в ТО-2, ТР, КР за цикл определяем по формуле (14);
![]() ; (14)
; (14)
ДпрКР – число дней простоя автобусов в КР определяем по формуле (15);
ДпрКР = Д'прКР + ДТ ; (15)
Д'прКР - нормативный простой автобусов в КР, принимаем Д'прКР = 20;
ДТ - дни транспортировки автобусов для КР в АРМ и обратно определяем по формуле (16);
ДТ = ![]() ; (16)
; (16)
LАРМ – расстояние до АРМ, км.;
LПС – суточный пробег при перегоне автобусов до АРМ, км.;
ДТ
=![]() ;
;
ДпрТО-ТР – удельный простой автобусов в ТО и ТР в днях на 1000 км пробега, принимаем ДпрТО-ТР = 0,4;
ДпрКР = 20+ 4 = 24;
К'4 – коэффициент корректирования продолжительности простоя в ТО и Р в зависимости от пробега с начала эксплуатации;
Для определения К'4 находим по формуле (17) усредненный корректирующий коэффициент КПРср характеризующий пробег с начала эксплуатации в долях от нормативного пробега до КР условно – «новых» автобусов, условно – «старых» автобусов, а также после КР автобусов – старых
![]() ; (17)
; (17)
где
![]() –
коэффициент корректирования пробега с начала эксплуатации в долях от
нормативного пробега до КР для условно – «новых» автобусов определяем по
формуле (18);
–
коэффициент корректирования пробега с начала эксплуатации в долях от
нормативного пробега до КР для условно – «новых» автобусов определяем по
формуле (18);
![]() =
=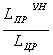 ; (18)
; (18)
![]() =
= ![]() ;
;
![]() – коэффициент
корректирования пробега с начала эксплуатации в долях от нормативного пробега
до КР для условно – «старых» автобусов определяем по формуле (19);
– коэффициент
корректирования пробега с начала эксплуатации в долях от нормативного пробега
до КР для условно – «старых» автобусов определяем по формуле (19);
![]() =
=![]() ; (19)
; (19)
![]() =
= ![]() ;
;
![]() – коэффициент
корректирования пробега с начала эксплуатации в долях от нормативного пробега
до КР для автобусов прошедших КР старых определяем по формуле (20);
– коэффициент
корректирования пробега с начала эксплуатации в долях от нормативного пробега
до КР для автобусов прошедших КР старых определяем по формуле (20);
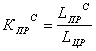 ; (20)
; (20)
![]() =
= ![]() ;
;
КПРср=![]() ;
;
по найденному значению КПРср, принимаем [8, с. 28] К'4= К4= 1,4;
![]() ;
;
Определяем коэффициент использования парка автобусов по формуле (21)
![]() , (21)
, (21)
Где Др.г. – число рабочих дней в году (по исходным данным);
ДКГ – число календарных дней в году;
Определяем коэффициент перехода от цикла к году по формуле (22)
![]() , (22)
, (22)
Определяем годовой пробег парка автобусов по формуле (23)
![]() , (23)
, (23)
Находим число КР по парку за год по формуле (24)
![]() , (24)
, (24)
![]()
![]() .
.
Находим число ТО-2 по парку за год по формуле (25)
![]() , (25)
, (25)
![]()
![]() .
.
Находим число ТО-1 по парку за год по формуле (26)
![]() , (26)
, (26)
![]()
![]() .
.
Находим число ЕО по парку за год по формуле (27)
![]() , (27)
, (27)
![]()
![]() .
.
Определение суточной программы по ТО автобусов
Суточная программа ЕО определяется по формуле (28)
NЕО сут =![]() , (28)
, (28)
где Др.з. – число рабочих дней в году соответствующей зоны ТО;
NЕО сут =![]() .
.
Суточная программа ТО-1 определяется по формуле (29)
N1 сут = ![]() , (29)
, (29)
N1 сут = ![]() .
.
Суточная программа ТО-2 определяется по формуле (30)
N2 сут = ![]() , (30)
, (30)
N2 сут = ![]() .
.
1.2.2 Расчет трудоемкости работ и численности производственных рабочих
Расчет годовой трудоемкости работ ТО
Принимаем нормативные трудоемкости [8, с. 15] для каждого вида ТО
tео = 0,95 чел.-ч.; t1 = 6,6 чел.-ч.; t2 = 25,8 чел.-ч.
Корректируем трудоемкости каждого вида ТО по формулам (31) – (33)
t'eo = teo ∙K2 ∙K5, (31)
где К2 – коэффициент корректирования трудоемкости ТО и ТР в зависимости от модели ПС и организации его работы, принимаем К2 =1,0;
К5 – коэффициент корректирования трудоемкости ТО и ТР в зависимости от количества обслуживаемых и ремонтируемых автобусов на ПАТП и количества технологически совместимых групп подвижного состава, принимаем К5 = 0,95;
t'eo
= ![]() ,
,
t'1 = t1∙K2∙∙K5 , (32)
t'1
= ![]() ,
,
t'2 = t2∙K2∙K5 , (33)
t'2 = ![]() .
.
Определяем годовую трудоемкость ЕО по формуле (34)
Тео = Nеог.∙t'ео , (34)
Тео
= ![]() .
.
Для определения годовой трудоемкости ТО-1 и ТО-2 необходимо рассчитать производственную программу Д-1 и Д-2.
Находим количество Д-1 за год по формуле (35)
NД1.г = 1,1∙N1г +N2г , (35)
NД1.г = ![]() .
.
Определяем суточную программу Д-1 по формуле (36)
NД1 сут = ![]() , (36)
, (36)
NД1 сут = ![]() .
.
Находим количество Д-2 за год по формуле (37)
NД2.г = 1,2∙N2г , (37)
NД2.г = ![]() .
.
Определяем суточную программу Д-2 по формуле (38)
NД2сут = ![]() , (38)
, (38)
NД2сут. = ![]() .
.
Поскольку контрольно-диагностические работы (КДР) и регулировочные работы (РР) при Д-1 входят в ТО-1, то расчетная трудоемкость ТО-1 уменьшается (при организации Д-1 на отдельных постах) на величину трудоемкости Д-1 (аналогично и для Д-2).
В связи с этим корректируем величину t1' по формуле (39)
t1" = t1'– tД1 , (39)
где tД1 = t1'∙0,12 (принимаем 12% от корректированной трудоемкости одного ТО-1);
tД1 = ![]() ;
;
t1" = ![]() .
.
Находим годовую трудоемкость Д-1 (ТД1) по формуле (40)
ТД1 = tД1 ∙NД1.г , (40)
ТД1
= ![]() .
.
Корректируем величину t2' по формуле (41)
t2"= t2' – tД2 - tД1, (41)
введено потому, что нужно учесть заключительные работы Д-1 при Д-2, где tД2 = t2'∙0,1, принимаем 10% от корректированной трудоемкости одного ТО-2;
tД2 = ![]() ;
;
t2" = ![]() .
.
Находим годовую трудоемкость Д-2 (ТД2) по формуле (42)
ТД2 = tД2∙ NД2.г , (42)
ТД2
= ![]() .
.
Определяем удельную трудоемкость ремонта сопутствующего ТО-1 по формуле (43)
tРС1 = 0,1∙t1", (43)
tРС1 = ![]() .
.
Определяем годовую трудоемкость ремонта сопутствующего ТО-1 по формуле (44)
TРС1 = NРС1∙tРС1 , (44)
где NРС1 – количество ремонтов сопутствующих ТО-1;
NРС1 = N1г= 3487;
TРС1 = ![]() .
.
Находим годовую трудоемкость ТО-1 по формуле (45)
T1 = N1г∙t1", (45)
T1 = ![]() .
.
Находим суммарную годовую трудоемкость ТО-1
T1' = T1 + TРС1,
T1' = ![]() .
.
Определяем удельную трудоемкость сезонного обслуживания по формуле (46)
tСО = t2"∙0,2 , (46)
tСО = ![]() .
.
Находим годовую трудоемкость сезонного обслуживания по формуле (47)
ТСО = 2∙АИ∙ tСО, (47)
ТСО = ![]() .
.
Определяем удельную трудоемкость ремонта сопутствующего ТО-2 по формуле (48)
tРС2 = 0,2∙t2", (48)
tРС2 = ![]() .
.
Определяем годовую трудоемкость ремонта сопутствующего ТО-2 по формуле (49)
TРС2 = NРС2∙tРС2 , (49)
где NРС2 – количество ремонтов сопутствующих ТО-2;
NРС2 = N2г = 1107;
TРС2 = ![]() .
.
Находим годовую трудоемкость ТО-2 по формуле (50)
T2 = N2г∙t2", (50)
T2 = ![]() .
.
Находим суммарную годовую трудоемкость ТО-2
T2' = T2 + TCO + TРС2 ,
T2'
= ![]() .
.
Годовая трудоемкость по всем видам ТО:
TТО = TЕО + T1' + T2' + TД1 + TД2
TТО = ![]() .
.
Расчет годовой трудоемкости работ ТР
Выбираем нормативную удельную трудоемкость для ТР:
tТР = 6,9 чел.-ч/1000 км
Корректируем трудоемкость ТР по формуле (51)
t'ТР = tТР∙К1∙К2∙К3∙К4∙К5 , (51)
где К1 – коэффициент корректирования удельной трудоемкости ТР в зависимости от условий эксплуатации, принимаем К1 = 1,1;
К3 – коэффициент корректирования удельной трудоемкости ТР в зависимости от природно-климатических условий, принимаем К3 = 1,0;
К4 – коэффициент корректирования удельной трудоемкости ТР, принимаем К4 = 1,4;
t'ТР = ![]() .
.
Удельная трудоемкость сокращается за счет выявления неисправностей при плановом диагностировании в предотказном состоянии.
Распределяем удельную трудоемкость на постовые и цеховые работы.
Находим удельную трудоемкость постовых работ по формуле (52)
t'ТР.П = t'ТР∙ППР, (52)
где ППР – процент постовых работ, принимаем ППР = 44 %;
t'ТР.П =![]() .
.
Находим удельную трудоемкость цеховых работ по формуле (53)
t'ТР.Ц = t'ТР ∙ПЦР, (53)
где ПЦР – процент цеховых работ, принимаем ПЦР = 56 %;
t'ТР.Ц =![]() .
.
Находим дважды скорректированную удельную трудоемкость цеховых работ по формуле (54)
t"ТР.Ц = 0,9∙t'ТР.Ц , (54)
t"ТР.Ц = ![]() .
.
Определяем годовую трудоемкость текущего ремонта по формуле (55)
ТТР=![]() , (55)
, (55)
ТТР= ![]() .
.
Определяем суммарные производственные годовые трудоемкости по ТО и ТР:
ТПР= ТТО+ТТР
ТПР=
![]() .
.
Рассчитаем годовую трудоемкость вспомогательных работ по формуле (56)
ТВСП = ТПР ∙КВСП , (56)
где КВСП – коэффициент вспомогательных работ;
КВСП = 0,25 при АИ до 300;
ТВСП
= ![]() .
.
Находим годовую трудоемкость самообслуживания по формуле (57)
ТСАМ = ТВСП ∙КСАМ , (57)
где КСАМ – коэффициент самообслуживания, принимаем КСАМ = 0,4;
ТСАМ
= ![]() .
.
Определяем суммарную годовую трудоемкость основных производственных и вспомогательных работ по АТП:
ТАТП = ТПР+ТВСП ,
ТАТП
= ![]() .
.
Расчет численности производственных рабочих
Определяем годовой фонд времени технологически необходимого (явочного) рабочего для шестидневной недели по формуле (58)
ФТ = ТСМ ∙(ДКГ – ДВ - ДП) – (ДПВ+ ДПП)∙2, (58)
где ТСМ – продолжительность рабочей смены, ч ТСМ = 7;
ДКГ – число календарных дней в году ДКГ = 365;
ДВ – число выходных дней в году ДВ = 52;
ДП – число праздничных дней в году ДП = 12;
ДПВ – число предвыходных дней в году ДПВ = 52;
ДПП - число предпраздничных дней в году ДПП = 5;
2 - сокращение рабочей смены в предвыходные и предпраздничные дни,ч.;
ФТ = 7∙(365-52-12) - (52+5)∙2 = 1993.
Определяем годовой фонд времени производственного штатного (списочного) рабочего по формуле (59)
ФШ = ТСМ ∙(ДКГ – ДВ - ДП – ДОТ – ДУП) – (ДПВ + ДПП)∙2, (59)
где ДОТ – число дней отпуска, дн., принимаем ДОТ = 24;
ДУП – потери рабочего времени по уважительным причинам (болезнь, выполнение государственных обязанностей и пр.), дн, принимаем ДУП =7;
ФШ = 7∙(365-52-12-24-7) – (52+5)∙2 = 1776.
Определяем численность технологически необходимого (явочного) числа рабочих по каждому виду воздействия
Находим численность рабочих для ЕО по формуле (60)
РТео = ![]() , (60)
, (60)
РТео = ![]() .
.
Находим численность рабочих для Д-1 по формуле (61)
РТд1 = ![]() , (61)
, (61)
РТд1 = ![]() .
.
Находим численность рабочих для Д-2 по формуле (62)
РТд2 = ![]() , (62)
, (62)
РТд2 = ![]() .
.
Находим численность рабочих для ТО-1 по формуле (63)
![]() =
= ![]() , (63)
, (63)
![]() =
= ![]() .
.
Определяем численность рабочих для ТО-2
Находим численность рабочих на постах по формуле (64)
![]() , (64)
, (64)
где ![]() – коэффициент затрат времени на
постах ТО-2, принимаем
– коэффициент затрат времени на
постах ТО-2, принимаем ![]() ;
;
![]() .
.
Находим численность рабочих в цехах по формуле (65)
![]() , (65)
, (65)
где ![]() – коэффициент затрат времени в
цехах, принимаем
– коэффициент затрат времени в
цехах, принимаем ![]() = 0,1;
= 0,1;
![]() =
= ![]()
![]() .
.
Численность рабочих на постах и в цехах составит:
![]() ,
,
![]() =
= ![]() .
.
Численность технологически необходимого числа рабочих занятых ТО:
РТто = РТео + РТд1 + РТд2 + РТт1 + РТт2 ,
РТто
= ![]() .
.
Определяем численность рабочих для ТР
Находим численность рабочих на постах по формуле (66)
![]() =
= ![]() , (66)
, (66)
где ![]() - коэффициент затрат времени на
постах ТР;
- коэффициент затрат времени на
постах ТР;
РТ.тр.п = ![]() .
.
Находим численность рабочих в цехах по формуле (67)
РТ.тр.ц = ![]() , (67)
, (67)
где ![]() - коэффициент затрат времени в
цехах ТР;
- коэффициент затрат времени в
цехах ТР;
РТ.тр.ц = ![]() .
.
Численность рабочих на постах и в цехах составит:
![]() ,
,
РТ.тр = ![]() .
.
Результаты расчетов сводим в таблицу 4.
Таблица 4 - Численность технологически необходимых рабочих
| №п/п | Вид воздействия | Численность персонала, чел | ||
| на постах | в цехах | всего | ||
| 1 | 2 | 3 | 4 | 5 |
| 1 | ЕО | 30 | - | 30 |
| 2 | Д-1 | 2 | - | 2 |
| 3 | ТО-1 | 13 | - | 13 |
| 4 | Д-2 | 2 | - | 2 |
| 5 | ТО-2 | 13 | 2 | 15 |
| 6 | ТР | 33 | 43 | 76 |
Определяем численность штатного (списочного) числа рабочих по каждому виду воздействия
Находим численность штатных рабочих занятых ТО по формуле (68)
РШ.то = ![]() , (68)
, (68)
РШ.то = ![]() .
.![]()
Находим численность штатных рабочих занятых ТР по формуле (69)
РШ.тр = ![]() , (69)
, (69)
РШ.тр = ![]() .
.
Находим коэффициент штатности для ТО по формуле (70)
![]() , (70)
, (70)
![]() .
.
Находим коэффициент штатности для ТР по формуле (71)
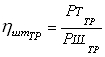 , (71)
, (71)
![]() .
.
Расчет годовой трудоемкости ТО и ТР.
Определяем трудоемкости постовых и цеховых работ для различных видов воздействия
Находим трудоемкость ЕО на постах по формуле (72)
![]() = ТЕО ∙
= ТЕО ∙![]() , (72)
, (72)
где ![]() – трудоемкость ЕО на постах;
– трудоемкость ЕО на постах;
![]() - коэффициент затрат времени на
постах ЕО, принимаем
- коэффициент затрат времени на
постах ЕО, принимаем ![]() = 1,0;
= 1,0;
![]() =
= ![]() .
.
Находим трудоемкость Д-1 на постах по формуле (73)
![]() = ТД1∙
= ТД1∙![]() , (73)
, (73)
где ![]() – трудоемкость Д-1 на постах;
– трудоемкость Д-1 на постах;
![]() - коэффициент затрат времени на
постах Д-1, принимаем
- коэффициент затрат времени на
постах Д-1, принимаем ![]() = 1,0;
= 1,0;
![]() =
= ![]() .
.
Находим трудоемкость Д-2 на постах по формуле (74)
![]() = ТД2∙
= ТД2∙![]() , (74)
, (74)
где ![]() – трудоемкость Д-2 на постах;
– трудоемкость Д-2 на постах;
![]() - коэффициент затрат времени на
постах Д-2, принимаем
- коэффициент затрат времени на
постах Д-2, принимаем ![]() = 1,0;
= 1,0;
![]() =
= ![]() .
.
Находим трудоемкость ТО-1 на постах по формуле (75)
![]() = Т1∙∙
= Т1∙∙![]() , (75)
, (75)
где ![]() – трудоемкость ТО-1 на постах;
– трудоемкость ТО-1 на постах;
![]() - коэффициент затрат времени на
постах ТО-1, принимаем
- коэффициент затрат времени на
постах ТО-1, принимаем ![]() = 1,0;
= 1,0;
![]() =
= ![]() .
.
Находим трудоемкость ТО-2 на постах по формуле (76)
![]() = Т2'
∙
= Т2'
∙![]() , (76)
, (76)
где ![]() – трудоемкость ТО-2 на постах;
– трудоемкость ТО-2 на постах;
![]() =
= ![]() .
.
Находим трудоемкость ТО-2 в цехах по формуле (77)
![]() = Т2'
∙
= Т2'
∙![]() , (77)
, (77)
где ![]() – трудоемкость ТО-2 в цехах;
– трудоемкость ТО-2 в цехах;
![]() =
= ![]() .
.
Находим трудоемкость ТР на постах по формуле (78)
![]() = ТТР
∙
= ТТР
∙![]() , (78)
, (78)
где ![]() – трудоемкость ТР на постах;
– трудоемкость ТР на постах;
![]() =
= ![]() .
.
Находим трудоемкость ТР в цехах по формуле (79)
![]() = ТТР
∙
= ТТР
∙![]() , (79)
, (79)
где ![]() – трудоемкость ТР в цехах;
– трудоемкость ТР в цехах;
![]() = 150884∙0,56=84495.
= 150884∙0,56=84495.
Результаты расчетов сводим в таблицу 5.
Таблица 5 - Трудоемкость постовых и цеховых работ для различных видов воздействия
| Вид воздействия | Трудоемкость по месту выполнения работ (чел.-ч) | |
| на постах | в цехах | |
| 1 | 2 | 3 |
| ЕО | 58582,8 | - |
| Д-1 | 4695,6 | - |
| ТО-1 | 26658,2 | - |
| Д-2 | 3254,6 | - |
| ТО-2 | 26783 | 2975,9 |
| ТР | 66371,4 | 84495 |
Определяем трудоемкости ТР и самообслуживания по видам работ и численности рабочих, занятых данным видом работ
Находим трудоемкость по каждому виду ТР на постах по формуле (80)
![]() , (80)
, (80)
где Ci - коэффициент затрат времени по данному виду работ.
Находим трудоемкость по каждому виду ТР в цехах по формуле (81)
![]() . (81)
. (81)
Находим численность рабочих по каждому виду работ ТР на постах по формуле (82)
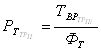 . (82)
. (82)
Находим численность рабочих по каждому виду работ ТР в цехах по формуле (83)
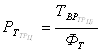 . (83)
. (83)
Результаты расчетов сводим в таблицу 6.
Таблица 6 - Трудоемкость и численность постовых и цеховых рабочих для ТР по видам работ
| № п/п | Виды работ | Ci (доля) |
|
|
|
| Постовые работы | |||||
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | Диагностические | 0,02 | 3016,9 | 1,51 | - |
| 2 | Регулировочные | 0,02 | 3016,9 | 1,51 | - |
| 3 | Разборочно-сборочные | 0,26 | 39219,4 | 19,68 | - |
| 4 | Сварочно-жестяницкие | 0,07 | 10559,1 | 5,3 | - |
| 5 | Малярные | 0,07 | 10559,1 | 5,3 | - |
| Итого | 0,44 | 66371,4 | 33,3 | - | |
| Цеховые работы | |||||
| 1 | Агрегатные | 0,17 | 25643,5 | - | 12,87 |
| 2 | Слесарно-механические | 0,08 | 12067,5 | - | 6,05 |
| 3 | Электротехнические | 0,08 | 12067,5 | - | 6,05 |
| 4 | Аккумуляторные | 0,01 | 1508,4 | - | 0,76 |
| 5 | Ремонт приборов системы питания | 0,03 | 4525,3 | - | 2,27 |
| 6 | Шиномонтажные | 0,03 | 4525,3 | - | 2,27 |
| 7 | Вулканизационные | 0,01 | 1508,4 | - | 0,76 |
| 8 | Кузнечно-рессорные | 0,03 | 4525,3 | - | 2,27 |
| 9 | Медницкие | 0,02 | 3016,9 | - | 1,51 |
| 10 | Сварочные | 0,015 | 2262,7 | - | 1,14 |
| 11 | Жестяницкие | 0,015 | 2262,7 | - | 1,14 |
| 12 | Арматурные | 0,04 | 6033,8 | - | 3,03 |
| 13 | Обойные | 0,03 | 4525,3 | - | 2,27 |
| Итого на общие работы | 0,56 | 84472,6 | - | 42,4 | |
| Всего на ТР | 1,0 | 150844 | 75,7 | ||
Находим трудоемкость по каждому виду работ самообслуживания по формуле (84)
![]() , (84)
, (84)
где Ci - коэффициент затрат времени по данному виду работ.
Находим численность рабочих по каждому виду работ самообслуживания по формуле (85)
![]() , (85)
, (85)
Результаты расчетов сводим в таблицу 7.
Таблица 7 - Трудоемкость и численность рабочих для самообслуживания
| № п/п | Виды работ | Ci (доля) |
чел.-ч |
|
|
| 1 | 2 | 3 | 4 | 5 | |
| 1 | Электромеханические | 0,25 | 8213,8 | 4,12 | |
| 2 | Механические | 0,1 | 3285,5 | 1,65 | |
| 3 | Слесарные | 0,16 | 5256,8 | 2,64 | |
| 4 | Кузнечные | 0,02 | 657,1 | 0,33 | |
| 5 | Сварочные | 0,04 | 1314,2 | 0,66 | |
| 6 | Жестяницкие | 0,04 | 1314,2 | 0,66 | |
| 7 | Медницкие | 0,01 | 328,5 | 0,16 | |
| 8 | Трубопроводные | 0,22 | 7228,1 | 3,63 | |
| 9 | Ремонтно – строительные и деревообрабатывающие | 0,16 | 5256,8 | 2,64 | |
| Итого на самообслуживание | 1,0 | 32855,2 | 16,49 | ||
Находим трудоемкость работ ТО-1 по агрегатам, системам и узлам по формуле (86)
ТТ1iАГР = Т1∙Ci, (86)
где Ci – коэффициент затрат времени по данному агрегату, системе, узлу.
Находим численность рабочих занятых ТО-1 агрегатов, систем и узлов по формуле (87)
РТ1iАГР = ![]() . (87)
. (87)
Примечание: Так как все работы по ТО-1 ведутся на постах, то расчет цеховых работ не производим.
Результаты расчетов сводим в таблицу 8.
Таблица 8 - Трудоемкость и численность рабочих, занятых работами ТО-1 по агрегатам, узлам и системам
| № п/п | Наименование агрегатов, систем, узлов и работ | Ci (доля) |
ТТ1iАГР, чел.-ч. |
РТ1iАГР, чел. |
||
| 1 | 2 | 3 | 4 | 5 | ||
| 1 | ДВС, система охлаждения и смазки | 0,035 | 933 | 0,47 | ||
| 2 | Система питания двигателя | 0,035 | 933 | 0,47 | ||
| 3 | Аккумуляторная батарея | 0,048 | 1272,6 | 064 | ||
| 4 | Генератор, стартер и реле-регулятор | 0,002 | 53,3 | 0,027 | ||
| 5 | Приборы освещения и сигнализации | 0,05 | 1332,9 | 0,67 | ||
| 6 | Сцепление | 0,007 | 186,6 | 0,094 | ||
| 7 | Коробка передач | 0,009 | 240 | 0,13 | ||
| 8 | Карданная передача | 0,02 | 533,2 | 0,27 | ||
| 9 | Задний мост | 0,03 | 799,7 | 0,4 | ||
| 10 | Рулевое управление и передний мост | 0,01 | 266,6 | 0,13 | ||
| 11 | Ножной тормоз | 0,052 | 1386,2 | 0,69 | ||
| 12 | Ручной тормоз | 0,02 | 533,2 | 0,27 | ||
| 13 | Ходовая часть и шины | 0,165 | 4398,6 | 2,2 | ||
| 14 | Кузов или платформа | 0,18 | 4798,4 | 2,4 | ||
| 15 | Оперение | 0,002 | 53,3 | 0,027 | ||
| Итого по агрегатам, узлам и системам | 0,665 | 17727,6 | 8,8 | |||
| Общие работы | ||||||
| 16 | Общий осмотр а/м | 0,02 | 533,2 | 0,27 | ||
| 17 | Смазочные и очистительные работы | 0,225 | 5998 | 3,0 | ||
| 18 | Уборочные работы | 0,05 | 1332,9 | 0,67 | ||
|
1 | 2 | 3 | 4 | 5 | |
|
19 | Моечные работы | 0,04 | 1066,3 | 0,53 | |
|
Итого на общие работы | 0,335 | 8930,4 | 4,47 | ||
|
Всего на ТО-1 | 1,0 | 26658 | 13,3 | ||
Находим трудоемкость работ ТО-2 по агрегатам, системам и узлам по формуле (88)
ТТ2iАГР = Т2'∙Ci, (88)
где Ci – коэффициент затрат времени по данному агрегату, системе, узлу.
Находим численность рабочих, занятых ТО-2 агрегатов, систем и узлов по формуле (89)
РТ2iАГР = ![]() , (89)
, (89)
Находим численность рабочих, занятых ТО-2 агрегатов, систем и узлов на постах по формуле (90)
РТ2iАГР.П = РТ2iАГР∙![]() , (90)
, (90)
Находим численность рабочих, занятых ТО-2 агрегатов, систем и узлов в цехах по формуле (91)
РТ2iАГР.Ц = РТ2iАГР∙![]() , (91)
, (91)
Результаты расчетов сводим в таблицу 9.
Таблица 9 - Трудоемкость и численность постовых и цеховых рабочих, занятых работами ТО-2 по агрегатам, узлам и системам
| № п/п | Наименование агрегатов, систем, узлов и работ | Ci (доля) |
ТТ2iАГР, чел.-ч. |
РТ2iАГР, чел. |
РТ2iАГР.П, чел. |
РТ2iАГР.Ц, чел. |
|||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| По агрегатам, узлам и системам | |||||||||
| 1 | ДВС, система охлаждения и смазки | 0,067 | 1993,8 | 1,0 | 0,9 | 0,1 | |||
| 2 | Система питания двигателя | 0,04 | 1190,4 | 0,6 | 0,54 | 0,06 | |||
| 3 | Аккумуляторная батарея | 0,035 | 1041,6 | 0,52 | 0,47 | 0,05 | |||
| 4 | Генератор, стартер и реле-регулятор | 0,034 | 1011,8 | 0,5 | 0,46 | 0,04 | |||
| 5 | Приборы освещения и сигнализации | 0,041 | 1220,1 | 0,61 | 0,55 | 0,06 | |||
| 6 | Сцепление | 0,01 | 297,6 | 0,15 | 0,13 | 0,02 | |||
| 7 | Коробка передач | 0,015 | 446,4 | 0,22 | 0,2 | 0,02 | |||
| 8 | Карданная передача | 0,015 | 446,4 | 0,22 | 0,2 | 0,02 | |||
| 9 | Задний мост | 0,015 | 446,4 | 0,22 | 0,2 | 0,02 | |||
| 10 | Рулевое управление и передний мост | 0,04 | 1190,4 | 0,6 | 0,54 | 0,06 | |||
| 11 | Ножной тормоз | 0,14 | 4166,2 | 2,1 | 1,88 | 0,022 | |||
| 12 | Ручной тормоз | 0,01 | 297,6 | 0,15 | 0,13 | 0,02 | |||
| 13 | Ходовая часть и шины | 0,14 | 4166,2 | 2,1 | 1,88 | 0,022 | |||
| 14 | Кузов или платформа | 0,22 | 6546,9 | 3,28 | 2,95 | 0,33 | |||
| 15 | Оперение | 0,005 | 148,8 | 0,075 | 0,067 | 0,008 | |||
| Итого по агрегатам, узлам и системам | 0,827 | 24610,5 | 12,3 | 11,1 | 1,2 | ||||
| Общие работы | |||||||||
| 16 | Общий осмотр а/м | 0,008 | 238 | 0,12 | 0,107 | 0,013 | |||
| 17 | Смазочные и очистительные работы | 0,125 | 3719,9 | 1,87 | 1,67 | 0,2 | |||
| 18 | Уборочные работы | 0,025 | 744 | 0,37 | 0,33 | 0,04 | |||
| 19 | Моечные работы | 0,015 | 446,4 | 0,22 | 0,2 | 0,02 | |||
| Итого на общие работы | 0,173 | 5148,3 | 2,58 | 2,32 | 0,26 | ||||
| Всего на ТО-2 | 1,0 | 29758,8 | 14,9 | 13,4 | 1,5 | ||||
Находим трудоемкость работ ТР по агрегатам, системам и узлам по формуле (92)
ТТРiАГР = ТТР∙Ci, (92)
где Ci – коэффициент затрат времени по данному агрегату, системе, узлу.
Находим численность рабочих, занятых ТР агрегатов, систем и узлов по формуле (93)
РТРiАГР = ![]() . (93)
. (93)
Находим численность рабочих, занятых ТР агрегатов, систем и узлов на постах по формуле (94)
ТТРiАГР.П = РТРiАГР ∙![]() . (94)
. (94)
Находим численность рабочих, занятых ТР агрегатов, систем и узлов в цехах по формуле (95)
ТТРiАГР.Ц = РТРiАГР ∙![]() , (95)
, (95)
Результаты расчетов сводим в таблицу 10.
Таблица 10 - Численность и трудоемкость постовых и цеховых рабочих, занятых ТР по агрегатам, узлам и системам
| № п/п | Наименование агрегатов, систем, узлов и работ | Ci (доля) |
ТТРiАГР, чел.-ч. |
РТРiАГР, чел. |
РТРiАГР.П, чел. |
РТРiАГР.Ц, чел. |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | ДВС, система охлаждения и смазки | 0,15 | 22632,6 | 11,3 | 5,0 | 6,3 |
| 2 | Система питания двигателя | 0,04 | 6035,4 | 3,1 | 1,33 | 1,77 |
| 3 | Аккумуляторная батарея | 0,02 | 3017,7 | 1,51 | 0,66 | 0,85 |
| 4 | Генератор, стартер и реле-регулятор | 0,04 | 6035,4 | 3,1 | 1,33 | 1,77 |
| 5 | Приборы освещения и сигнализации | 0,03 | 4526,5 | 2,27 | 1,0 | 1,27 |
| 6 | Сцепление | 0,03 | 4526,5 | 2,27 | 1,0 | 1,27 |
| 7 | Коробка передач | 0,03 | 4526,5 | 2,27 | 1,0 | 1,27 |
| 8 | Карданная передача | 0,025 | 3772,1 | 1,9 | 0,83 | 1,07 |
| 9 | Задний мост | 0,03 | 4526,5 | 2,27 | 1,0 | 1,27 |
| 10 | Рулевое управление и передний мост | 0,06 | 9053 | 4,54 | 2,0 | 2,54 |
| 11 | Ножной тормоз | 0,1 | 15088,4 | 7,57 | 3,33 | 4,24 |
| 12 | Ручной тормоз | 0,02 | 3017,4 | 1,51 | 0,66 | 0,85 |
| 13 | Ходовая часть и шины | 0,12 | 18106,1 | 9,1 | 4,0 | 5,1 |
| 14 | Кузов или платформа | 0,119 | 17955,2 | 9,0 | 3,96 | 5,04 |
| 15 | Оперение | 0,001 | 150,88 | 0,076 | 0,033 | 0,043 |
| 16 | Слесарно-механические работы | 0,11 | 16597,2 | 8,33 | 3,66 | 4,67 |
| 17 | Прочие работы (малярные и др.) | 0,075 | 11316,3 | 5,68 | 2,5 | 3,18 |
| Итого на ТР | 1,0 | 150884 | 75,7 | 33,3 | 42,4 | |
Используя данные таблицы 8, сформируем цеха ТР в соответствии со спецификой работ и определим численность цеховых рабочих.
Таблица 11 - Численность рабочих в цехах ТР
| Наименование цеха | Численность рабочих по расчетам, чел. | Принятая численность рабочих, чел. |
| Моторный | 6,3 | 6 |
| Цех топливной аппаратуры | 1,77 | 2 |
| Аккумуляторный цех | 0,85 | 2 |
| Электротехнический | 3,04 | 3 |
| Агрегатный | 11,26 | 11 |
| Шиномонтажный | 2,3 | 2 |
| Вулканизационный | 2,2 | 2 |
| Кузовной с отделением сварочно-жестяницким | 5,08 | 5 |
| Обойный | 1,2 | 1 |
| Медницкий | 1,1 | 1 |
| Тепловой | 1,3 | 1 |
| Слесарно-механический | 4,67 | 5 |
| Малярный | 1,2 | 1 |
| Нестандартного оборудования | 1,2 | 2 |
1.2.3 Расчет числа постов
Определение числа постов зон ТО
Рассчитываем число постов зоны ЕО
Находим ритм производства по формуле (96)
REO = ![]() , (96)
, (96)
где ТСМ – продолжительность смены, ч;
nСМ – число смен;
NСУТ.ЕО – суточная программа зоны;
REO = ![]() .
.
Определяем такт линии непрерывного действия по формуле (97)
τЛ.EO= ![]() , (97)
, (97)
где Lа – габаритная длина автобуса, м;
а – расстояние между автобусами на постах линии, м;
Vк – скорость конвейера непрерывного действия, м/мин;
τЛ.EO= ![]() .
.
Находим число линий по формуле (98)
mEO = ![]() , (98)
, (98)
mEO = ![]() .
.
Определяем пропускную способность линии ЕО по формуле (99)
![]() , (99)
, (99)
![]() .
.
Рассчитываем число постов зоны ТО-1
Находим ритм зоны по формуле (100)
R1 = ![]() , (100)
, (100)
R1 = ![]() .
.
Определяем такт линии периодического действия по формуле (101)
τл.1
= ![]() + tП, (101)
+ tП, (101)
где t”1 – корректированная нормативная трудоемкость одного обслуживания ТО-1, чел.-ч.;
ХЛ – число постов на линии;
tП – время передвижения автобуса с поста на пост;
PСР – среднее число рабочих, одновременно занятых на одном посту, чел;
τл.1 = ![]() .
.
Находим число линий по формуле (102)
Nл.1 = ![]() , (102)
, (102)
Nл.1 = ![]() .
.
Определяем пропускную способность линии ТО-1 по формуле (103)
![]() , (103)
, (103)
![]() .
.
Рассчитываем число постов зоны ТО-2
Находим ритм зоны по формуле (104)
R2 = ![]() , (104)
, (104)
R2 = ![]() .
.
Определяем такт поста по формуле (105)
τП.2
= ![]() + tП, (105)
+ tП, (105)
где t″2 – корректированная нормативная трудоемкость одного обслуживания ТО-2, чел.-ч.;
PСР – среднее число рабочих, одновременно занятых на одном посту, чел;
τП.2 = ![]() .
.
Находим число постов по формуле (106)
n2 = ![]() , (106)
, (106)
n2 = ![]() .
.
Рассчитываем число постов зоны Д-1
Находим ритм зоны по формуле (107)
RД1 = ![]() , (107)
, (107)
R Д1 = ![]() .
.![]()
Определяем такт поста по формуле (108)
τП.Д1 = ![]() + tП, (108)
+ tП, (108)
где tД1 – корректированная нормативная трудоемкость одного обслуживания Д-1, чел.-ч.;
τ
П.Д1 = ![]() .
.
Находим число постов по формуле (109)
nД1 = ![]() , (109)
, (109)
nД1 = ![]() .
.
Рассчитываем число постов зоны Д-2
Находим ритм зоны по формуле (110)
RД2 = ![]() , (110)
, (110)
R Д2 = ![]() .
.
Определяем такт поста по формуле (111)
τ
П.Д2 = ![]() + tП , (111)
+ tП , (111)
где tД2 – корректированная нормативная трудоемкость одного обслуживания Д-2, чел.-ч.;
τ
П.Д2 = ![]() .
.
Находим число постов по формуле (112)
nД2 = ![]() , (112)
, (112)
nД2 = ![]() .
.
Рассчитываем число постов зоны ТР по формуле (113)
nТР=![]() , (113)
, (113)
где Ттр п- трудоемкость ТР на постах;
Кн.п - коэффициент, учитывающий неритмичность подачи автомобилей на ремонт;
η п - коэффициент использования рабочего времени поста;
n см - число смен;
Рср - среднее число рабочих на посту;
![]() .
.
1.3 Организационная часть
1.3.1 Выбор метода организации технологического процесса ТО и ТР
Организация того или иного метода ТО и ТР зависит от суточной программы и продолжительности технических воздействий.
Принимаем согласно расчетам для уборочно-моечных работ ЕО две поточные линии непрерывного действия, каждая из которых состоит из трех постов. На первом посту производится внутренняя уборка автобуса и внешняя очистка от грязи (снега), на втором – автоматизированная мойка, на третьем – домывка и обтирка. Пропускная способность двух линий по расчету составляет 26 авт/ч, что достаточно для выполнения суточной программы ЕО.
Так как суточная программа ТО-1 составляет 12 автобусов, то наиболее целесообразна организация проведения ТО-1 на трехпостовой поточной линии периодического действия с двумя дополнительными постами (ожидания и контроля). Пропускная способность линии позволяет выполнить программу за семичасовую рабочую смену.
ТО-2 организуем на четырех универсальных тупиковых постах методом комплексных бригад.
В связи с тем, что в автотранспортном предприятии насчитывается 205 автобусов целесообразно проведение Д-1 и Д-2 в отдельных зонах. Зоны Д-1 и Д-2 имеют по два проездных поста, расположенных в линию и пост ожидания.
Зоны диагностики снабжены высокопроизводительными автоматизированными диагностическими средствами.
Основываясь на расчетных данных организуем ТР автобусов на шести универсальных тупиковых постах методом комплексных бригад.
Рабочие, обслуживающие зону ЕО работают 365 дней в году по скользящему графику.
Рабочие остальных зон и цехов работают 302 дня в году по шестидневной рабочей неделе.
Текущий ремонт автобусов производится агрегатно-узловым методом, позволяющим сократить время простоя автобуса в ремонте.
В связи с тем, что работы зон ЕО и ТО-1 проводятся в ночные часы, предусматривается чередование сменами и постами с другими зонами при помощи комплексных бригад.
1.3.2 Определение режима работы зон ТО и ТР
Продолжительность межсменного времени при равномерном выпуске автобусов определяем по формуле (114)
Тмс = 24 - (Тн - Тв), (114)
где Тн – продолжительность работы автобусов в наряде, ч, принимаем Тн =16;
Тв – продолжительность выпуска автобусов на линию, определяем по формуле (115);
![]() ; (115)
; (115)
А'и – число автобусов, выезжающих на линию находим по формуле (116);
![]() =Аи∙αТ; (116)
=Аи∙αТ; (116)
![]() =
=![]() ;
;
tвып – время выпуска каждого автобуса, мин, принимаем tвып = 2;
Пся – число смотровых ям на контрольно-техническом пункте, принимаем Пся = 4;
![]() ;
;
Тмс=![]() .
.
По результатам расчета построим график суточной работы автобусов и зон ТО и ТР, представленный на рисунке 1.
|
|
|||||||||
| | | | | | | | | | | | | | | | | | | | | | | | | |||||||||
| Рабочие смены | 3-я | 1-я | 2-я | ||||||
| Работа на линии | |||||||||
| Работа зоны ЕО | |||||||||
| Работа зон ТО-1, Д-1 | |||||||||
| Работа зон ТО-2, Д-2 | |||||||||
| Работа зоны ТР | |||||||||
Рисунок 1 - График суточной работы автомобилей и зон ТО и ТР
Принимаем:
время выезда 1-го автобуса 500;
время работы зоны ЕО с 2100 до 500;
время работы зоны ТО-1 и Д-1 с 2115 до 515;
время работы зоны ТО-2 и Д-2 с 800 до 1600;
время работы зоны ТР с 800 до 1600; с 1600 до 2400; с 2400 до 800.
1.3.3 Расчет площадей объектов ПАТП
Определение площади зон ТО и ТР
Находим удельную площадь приходящуюся на 1 пост по формуле (117)
FУД = КА1Аа∙ППа , (117)
где КА1Аа – отношение проекций автобуса по заданию к аналогу;
КА1Аа = ![]() ;
;
ПА1 – проекция автобуса по заданию (ЛАЗ-4207), м2;
ПА1 = ![]() ;
;
ППа – полезная удельная площадь на 1 ед. автобуса аналога, принимаем ППа = 44,9 м 2;
ПАа – проекция автобуса аналога (ЛАЗ-695), м2;
ПАа = ![]() ;
;
КА1Аа = ![]() ;
;
FУД = 1,2∙63,5= 70.
Определим удельную строительную площадь поста по формуле (118)
FУД.СТР = FУД ∙КСТР , (118)
где КСТР - коэффициент зависящий от расположения поста относительно ворот, принимаем КСТР = 1,15;
FУД.СТР = ![]() .
.
Определяем удельную строительную площадь зон ТО и ТР
Находим удельную строительную площадь зоны ЕО по формуле (119)
FУД.СТР.ЕО = FУД.СТР ∙nЕО, (119)
FУД.СТР.ЕО = ![]() .
.
Находим удельную строительную площадь зоны Д-1 по формуле (120)
FУД.СТР.Д1 = FУД.СТР∙nД1, (120)
FУД.СТР.Д1 = ![]() .
.
Находим удельную строительную площадь зоны Д-2 по формуле (121)
FУД.СТР.Д2 = FУД.СТР∙nД2, (121)
FУД.СТР.Д2 = ![]() .
.
Находим удельную строительную площадь зоны ТО-1 по формуле (122)
FУД.СТР.Т1 = FУД.СТР∙nТ1, (122)
FУД.СТР.Т1 = ![]() .
.
Находим удельную строительную площадь зоны ТО-2 по формуле (123)
FУД.СТР.Т2 = FУД.СТР∙nТ2, (123)
FУД.СТР.Т2 = ![]() .
.
Находим удельную строительную площадь зоны ТР по формуле (124)
FУД.СТР.ТР = FУД.СТР∙nТР , (124)
FУД.СТР.ТР = ![]() .
.
Результаты расчетов сводим в таблицу 12.
Таблица 12 - Площади зон ТО и ТР
| № п/п | Наименование зон (участков) ТО и ТР |
Удельная строительная площадь поста, м2 |
Число постов |
Расчетная площадь зон (участков), м2 |
Принятая площадь зон (участков), м2 |
|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ЕО | 81 | 6 | 486 | 504 | |
| 2 | Д-1 | 81 | 2 | 162 | 252 | |
| 3 | Д-2 | 81 | 2 | 162 | 252 | |
| 4 | ТО-1 | 81 | 3+2 | 405 | 432 | |
| 5 | ТО-2 | 81 | 4 | 324 | 340 | |
| 6 | ТР | 81 | 6 | 486 | 490 | |
Определение площади цехов
Находим площади цехов по удельной площади на одно рабочее место (одного рабочего) по формуле (127)
Fц - площадь цеха (участка);
FР1 – удельная площадь на первое рабочее место (рабочего), м2;
FР2 – удельная площадь на каждое последующее рабочее место (рабочего), м2;
Рм – число рабочих мест в цехе.
Определим площадь моторного цеха:
FМ = ![]() .
.
Определим площадь цеха топливной аппаратуры:
FтА = ![]() .
.
Определим площадь электротехнического цеха:
FЭ = ![]() .
.
Определим площадь аккумуляторного цеха:
FАК = ![]() .
.
Определим площадь шиномонтажного цеха:
Fш = 15 + 10∙(2-1) = 25.
Определим площадь вулканизационного цеха:
FВ = ![]() .
.
Определим площадь медницкого цеха:
FМД = ![]() .
.
Определим площадь кузовного цеха с отделением сварочно-жестяницким:
Fк = ![]() .
.
Определим площадь слесарно-механического цеха:
FСМ = ![]() .
.
Определяем площадь малярного цеха с учетом ввода в него автобуса:
FМАЛ = ![]() .
.
Определим площадь теплового цеха:
Fк= ![]() .
.
Определим площадь цеха нестандартного оборудования:
Fн.об = ![]() .
.
Определим площадь обойного цеха:
FОБ = ![]() .
.
Находим площадь агрегатного цеха по коэффициенту плотности оборудования по формуле (125)
FА = Кп∙∑ Fоб , (125)
где Кп – коэффициент плотности оборудования агрегатного цеха, принимаем Кп = 4,5;
∑ Fоб – суммарная площадь оборудования агрегатного цеха, принимаем ∑ Fоб = 31,6;
FА = ![]() .
.
Примечание: Считается целесообразным увеличить площади цехов в связи с дальнейшим развитием предприятия.
Результаты расчетов сводим в таблицу 13.
Таблица 13 - Площади цехов
| № п/п | Наименование цеха | Численность цеховых рабочих |
Расчетная площадь цеха,м2 |
Принятая площадьцеха,м2 |
||
| 1 | 2 | 3 | 4 | 5 | ||
| 1 | Моторный | 6 | 75 | 90 | ||
| 2 | Цех топливной | 2 | 12 | 31 | ||
| аппаратуры | ||||||
| 3 | Электротехнический цех | 3 | 20 | 36 | ||
| 4 | Аккумуляторный | 2 | 25 | 36 | ||
| 5 | Агрегатный | 11 | 142 | 143 | ||
| 7 | Шиномонтажный | 2 | 25 | 30 | ||
| 8 | Вулканизационный | 2 | 25 | 27 | ||
| 9 | Кузовной | 3 | 78 | 94 | ||
| 10 | Обойный | 1 | 15 | 25 | ||
| 11 | Медницкий | 1 | 12 | 36 | ||
| 12 | Слесарно-механический | 5 | 52 | 65 | ||
| 13 | Малярный | 2 | 30 | 75 | ||
| 14 | Тепловой | 1 | 20 | 36 | ||
| 15 | Нестандартного оборудования | 2 | 22 | 32 | ||
1.3.4 Технологическое проектирование агрегатного цеха
Агрегатный цех предназначен для выполнения ремонта узлов и агрегатов в основном путем замены неисправных деталей новыми или ранее отремонтированными.
Площадь цеха:
- расчетная – 142 м2;
- принятая – 143 м2.
Численность рабочих в цехе:
- расчетная – 11,2 чел;
- принятая – 11 чел.
Цех работает в одну смену по пятидневной рабочей неделе.
Продолжительность смены: 8 ч., плюс 1 ч. перерыва (с 800 до 1700).
Агрегатный цех производит ремонт сцепления, коробки передач, карданной передачи, заднего и переднего мостов, рулевого управления автобусов. Частично в этом же цеху восстанавливают детали большей частью слесарным инструментом. Общий для большинства агрегатов технологический процесс ремонта включает: мойку агрегата; подразборку в соответствии с объемом ремонта; мойку снятых деталей и их дефектовку; комплектовку деталей после ремонта из запасных частей; сборку и испытания агрегатов.
Разборочно – сборочные работы в агрегатном цехе проводят на специальных стендах, обеспечивающих возможность подхода к ремонтируемому агрегату с разных сторон, а также поворот и наклон агрегата для удобства работы. Стенды специализированы по типам агрегатов. Они размещаются в зоне действия кран-балки. Для размещения и разборки снятых с агрегатов узлов предусмотрены слесарные верстаки, столы и стеллажи. Кроме обычных ключей различного типа при разборочно – сборочных работах применяются гайковерты различные съемники и приспособления.
Контроль, сортировку и комплектовку деталей производят с помощью измерительного инструмента и отдельных специальных приборов.
Испытания агрегатов после ремонта производят на специальных стендах.
Цех окрашен в светлые и спокойные тона, вентилируется приточно – вытяжной вентиляцией и имеет смешанное освещение (естественное и искусственное).
Условия труда в цеху соответствуют санитарным нормам, эстетическим требованиям и условиям безопасности.
Произведем подбор технологического оборудования агрегатного цеха и составим таблицу 14
Таблица 14 - Технологическое оборудование агрегатного цеха
| Наименование оборудования | Тип или модель | Габариты в плане, мм | Кол-во |
| 1 | 2 | 3 | 4 |
| Станок для расточки тормозных барабанов | ЦКБ-Р-114 | 1080∙830 | 1 |
| Радиально-сверлильный настольный станок | НРС-15 | 360∙360 | 1 |
| Стенд для разборки и регулировки сцеплений | ЦКБ-Р-207 | 526∙863 | 1 |
| Гидравлический пресс 40т | 2135-1М | 1520∙840 | 1 |
| Стенд для ремонта редукторов задних мостов | Р-284 | 740∙482 | 1 |
| Стенд для клепки тормозных накладок | Р-304 | 600∙430 | 1 |
| Стенд для ремонта коробок передач | 2365 | 500∙780 | 1 |
| Стенд для ремонта передних и задних мостов | 2450 | 1020∙780 | 1 |
| Настольно – верстачный пресс 3т | ОКС-918 | 920∙220 | 1 |
| Стенд для испытаний коробок передач | АКТБ-25А | 2400∙920 | 1 |
| Стенд для ремонта карданных валов | 3067 | 936∙600 | 1 |
| Заточный станок | И-138А | 860∙550 | 1 |
| Вертикально – сверлильный станок | 2А-125 | 1000∙800 | 1 |
| Подвесная кран-балка | ПТ-054 | 9000∙1500 | 1 |
Произведем подбор технологической оснастки агрегатного цеха и составим таблицу 15.
Таблица 15 - Технологическая оснастка агрегатного цеха
| Наименование оснастки | Модель | Кол-во |
| 1 | 2 | 3 |
| Прибор для измерения радиального зазора в подшипниках качения | КН-1223 | 1 |
| Универсальный комплект съемников и приспособлений для разборки и сборки узлов автобусов | УКАСП-58, ПИМ-192 | 1 |
| Комплект оправок для выполнения работ | - | 1 |
| Пневматический гайковерт | ГМП-14 | 3 |
| Большой набор гаечных ключей | И-105-М (1,2,3) | 3 |
| Напильники разные | - | 20 |
| 1 | 2 | 3 |
| Шаберы разные | - | 6 |
| Комплект инструментов слесаря | 2446 | 5 |
Произведем подбор организационной оснастки агрегатного цеха и составим таблицу 16.
Таблица 16 - Организационная оснастка агрегатного цеха
| Наименование оснастки | Тип или модель | Габариты в плане, мм | Кол-во |
| Верстак слесарный | СД-3701-04 | 1250∙800 | 3 |
| Стеллаж для деталей | ОРГ-1468-05-230А | 1400∙500 | 1 |
| Ларь для обтирочных материалов | ОРГ-1468-07-090А | 800∙400 | 1 |
| Ларь для отходов | ОРГ-1468-07-090А | 800∙400 | 1 |
| Стеллаж для инструментов | ОРГ-1468-05-280 | 1400∙500 | 2 |
| Шкаф настенный для приборов и инструментов | ОРГ-1468-07-010А | 500∙400 | 2 |
| Передвижная моечная ванна | ОМ-13116 | 1250∙620 | 1 |
| Стол для дефектовочных работ | ОРГ-1468-04-200 | 1600∙700 | 1 |
Расчет электроэнергии потребляемой агрегатным цехом
Определяем годовой расход силовой энергии по формуле (126)
WЭ = Д РГ∙ТСМ∙К ИЭ∙NЭ, (126)
где Д РГ - дни работы цеха в году, принимаем Д РГ = 302дня;
ТСМ – продолжительность смены, принимаем ТСМ = 8ч;
К ИЭ – коэффициент использования электрооборудования в течении смены. Для оборудования периодического действия принимаем К ИЭ = 0,1;
NЭ – суммарная мощность электрооборудования в агрегатном цехе;
WЭ = 302∙8∙0,1∙69,6 = 16815,2 кВт∙ч.
Определяем годовой расход осветительной электроэнергии по формуле (127)
WОС = q∙FА ∙Д РГ∙ТОСВ, (127)
где q∙- удельная плотность осветительной нагрузки, принимаем q∙= 25Вт / м2;
FА - площадь агрегатного цеха, м2;
ТОСВ – длительность работы светильников в течении смены, с учетом того, что в агрегатном цехе есть также естественное освещение, принимаем ТОСВ = 6ч;
WОС = 25∙143∙302∙6 = 6477900 Вт / ч = 6477,8 кВт / ч.
Находим общий годовой расход электроэнергии:
WОБЩ = WЭ + WОС,
WОБЩ = 16815,2 + 6477,8 = 23293 кВт / ч.
Расчет расхода воды в агрегатном цехе
Находим расход питьевой воды за год по формуле (128)
VП = q n∙Д РГ ∙РШ , (128)
где q n - расход воды на санитарно - бытовые нужды на одного человека в день, принимаем q n = 25л;
РШ – штатное число рабочих в наиболее нагруженную смену, чел;
VП = 25∙302∙11 = 83050 л, = 83,05 м3
Расчет расхода топлива на отопление агрегатного цеха
Отопление агрегатного цеха осуществляется от котельной расположенной на ПАТП.
Находим расход тепла за год на отопление агрегатного цеха по формуле (129)
Q = НТ∙ФОТ∙VН , (129)
где НТ - удельный расход тепла на отопление цеха, принимаем НТ = 12 ккал/м 3;
ФОТ - длительность отопительного сезона в течении года. С учетом того, что ПАТП находится в умеренной климатической зоне, ФОТ = 4200 m;
VН - объем части главного производственного корпуса приходящийся на агрегатный цех определяем по формуле (130);
VН = FА ∙Н ЗД ; (130)
где НЗД – высота здания, м;
VН = 143∙5 = 715 м3;
Q = 12∙4200∙715 = 36,036∙10 6 ккал.
Находим годовой расход топлива на отопление агрегатного цеха по формуле (131)
![]() , (131)
, (131)
где q – теплотворная способность 1 кг топлива. При применении в качестве топлива мазута, q = 89500 ккал/кг;
![]() кг.
кг.
Расчет искусственного освещения агрегатного цеха
Расчет проводим по методу
коэффициента использования светового потока. Количество ламп в светильниках
рассчитываем по формуле (132)![]()
![]() , (132)
, (132)
где Е – минимальная освещенность, принимаем300 лк;
К – коэффициент запаса, принимаем К = 1,5
S – площадь помещения, м2;
Z – коэффициент неравномерности освещения, принимаем Z = 1,1;
Ф – световой поток одной лампы, принимаем Ф = 4070лм для лампы
ЛО 80 люминесцентной дневного света, мощностью 80 Вт;
![]() - коэффициент равный отражению
светового потока, падающего на расчетную поверхность к световому потоку,
испускаемому лампами, принимаем
- коэффициент равный отражению
светового потока, падающего на расчетную поверхность к световому потоку,
испускаемому лампами, принимаем ![]() = 0,2 при коэффициентах отражения
потолка и стен pn=50, pст=30
= 0,2 при коэффициентах отражения
потолка и стен pn=50, pст=30
(известь, побеленный потолок, стены обклеены светлыми обоями).
Определяем индекс помещения по формуле (133)
![]() , (133)
, (133)
где Н, В – длина и ширина помещения, м;
Н р – высота подвеса светильников над рабочей поверхностью, определяется по формуле (134);
Н р = Н - h p - h с; (134)
h p – высота рабочей поверхности над полом, принимаем h p = 0,8 м;
h с – расстояние светового центра светильников от пола, принимаем
h с = 0,6 м;
Н р = 5 – 0,8 - 0,6 = 3,6 м;
![]() ;
;
![]() .
.
Выбираем для ламп пылевлагозащитные светильники ПВП1-2 в количестве 43 штук.
Для обеспечения нормируемой освещенности в агрегатном цехе необходимо установить 43 светильника ПВП1-2 с двумя лампами ЛД 80 (дневного света) в каждом светильнике. Светильники подвешивать на высоте 4,4 м. Тип электропроводки ПВВГ.
Расчет заземления производственного оборудования агрегатного цеха
Сопротивление растеканию тока RВ от одиночного вертикального заземления, помещенного на глубину tо определяется по формуле (135)
![]() , (135)
, (135)
где Ррас - расчетное удельное сопротивление грунта, Ом∙м;
ℓ – длина вертикального заземлителя, м;
d – наружный диаметр заземлителя, м
t – расстояние от середины заземлителя до поверхности грунта, определяем по формуле (136);
![]() , (136)
, (136)
В цехе работают электрические установки напряжением 380 В.
В качестве электродов используем стальные трубы ℓ = 2,5 м, Ø = 50мм,
соединенные между собой стальной полосой 4х40 мм, шаг заземлителей 3 м, заглубление соединительной полосы 0.8 м, грунт сухой песок.
![]() .
.
Находим удельное сопротивление грунта по формуле (137)
Ррас = Р∙Ψ, (137)
где Ррас – удельное сопротивление грунта, Ом∙м;
Ψ – коэффициент сезонности, учитывающий повышение сопротивления грунта в году;
Ррас = 83∙1,3 = 108 Ом∙м;
![]() ,
,
Находим число вертикальных заземлителей по формуле (138)
![]() , (138)
, (138)
где Rдоп = 4 Ом
![]() ,
,
Находим число вертикальных заземлителей с учетом η в по формуле (139)
![]() , (139)
, (139)
где η в коэффициент характеризующий уменьшение проводимости заземлителей или коэффициент экранирования, принимаем η в = 0,7
![]()
Определяем сопротивление соединительной полосы по формуле (140)
![]() , (140)
, (140)
где L – длина полосы, м;
B – ширина полосы, м.
![]() = 4,78 Ом
= 4,78 Ом
Находим общее сопротивление заземлительного устройства по формуле (141)
![]() , (141)
, (141)
![]() ,
,
Общее сопротивление заземлительного устройства меньше допустимого Rдоп = 4 Ом. Значит число вертикальных заземлителей остается прежним n = 12.
В качестве электродов предусмотрено использовать стальные трубы L = 2,5 м, d = 50 мм, соединенные между собой стальной полосой 4х40 мм, шаг заземлителей 3 м, заглубление 0,8 м. Все корпуса электродвигателей, распределительных коробов, светильников присоединить к заземляющему контуру.
ЗАКЛЮЧЕНИЕ
Преобразования социально-экономической реальности влекут за собой изменения требований к качеству профессиональной подготовки обучающихся начальной и средней профессиональной школы. Быстро меняющееся общество, увеличивающийся объем информации, непредсказуемость, усложнение в самом обществе между различными системами требуют формирования личности, соответствующей этим условиям.
Одной из современных тенденций системы профессионального образования является непрерывность, представляющая собой систему взаимодействующих образовательных программ, направленных на обеспечение и дальнейшее развитие профессиональных качеств выпускника в соответствии с его личностными потребностями и социально-экономическими требованиями.
Необходимость в непрерывном профессиональном образовании порождена усложнением профессиональной деятельности в период научно-технической революции, а также тем обстоятельством, что в условиях современного общества, основанного на знании, формирование мобильного и конкурентоспособного специалиста приобрело в настоящее время характер актуальной практической задачи.
Обобщение представленного в дипломной работе позволяет сформулировать следующие выводы.
В результате рассмотрения методологии исследования, истории развития и становления непрерывного профессионального образования, были уточнены основные понятия, сформировано обоснование, раскрыты социально-педагогические предпосылки разработки модели непрерывного профессионального образования в системе «ПУ –колледж».
На основании теоретического анализа научной (философской, педагогической, психологической, социологической) литературы уточнены понятия «непрерывное профессиональное образование», «преемственность в профессиональном образовании», «конкурентоспособный выпускник системы НПО-СПО».
В отечественной науке проблемам непрерывного образования посвящены труды И.В. Бестужева-Лады, Л.П. Буева, А.А. Вербицкого, С.Г. Вершловского, А.П. Владиславлева, Б.С. Гершунского, А.В. Даринского, О.В. Купцова, П.В. Лепина, В.Г. Онушкина, Ф.И. Перегудова, В.Н. Турченко, Ф.Г. Филиппова и др. Понятие «непрерывное образование» представлено как многогранное понятие: условие (и процесс) разностороннего развития личности, роста сущностных сил и способностей; реально-функционирующая система государственных и дополнительных образовательных учреждений; важнейший социально-педагогический принцип развития системы образования и др.
В целом, непрерывность профессионального образования обеспечивает возможность многомерного движения личности в образовательном пространстве и создания для нее оптимальных условий для этого движения.
Системообразующим фактором непрерывного профессионального образования выступает его целостность, т. е. глубокая интеграция всех подсистем и процессов профессионального образования. Это обеспечивается, прежде всего, преемственностью всех сторон учебно-воспитательного процесса, направленного на развитие личности. Реализацию принципа преемственности можно рассматривать в качестве основного механизма разрешения противоречия между дискретностью системы профессионального образования и необходимостью сохранения и обеспечения его целостности.
Таким образом, в результате выполненного теоретического и экспериментального исследования достигнута поставленная цель и решены задачи.
По результатам расчета количество технических обслуживаний по парку в год составило:
NЕО.г=65092 ед., NД1.г=4942,7 ед., N1Г=3487 ед., NД2.г=1328,4 ед., N2Г=1107 ед.
Трудоемкость в зонах ЕО, Д-1, ТО-1, Д-2, ТО-2 и ТР:
ТЕО=58582,8 чел.-ч., ТД1=4695,6 чел.-ч., ТТ1=26658,2 чел.-ч., ТД2=3254,6 чел.-ч., ТТ2.п=26783 чел.-ч., ТТР.п=66371,4 чел.-ч.
Трудоемкость цеховых работ:
ТТ2.ц=2975,9 чел.-ч., ТТР.ц=84495 чел.-ч.
Трудоемкость производственных и вспомогательных работ:
Тпр = 273794 чел.-ч., Твсп = 82138,2 чел.-ч.
Трудоемкость самообслуживания ТСАМ = 32855,3 чел.-ч.
Текущий ремонт автобусов организован в 3 смены: с 800 до 1600; с 1600 до 2400; с 2400 до 800 на 6 тупиковых постах канавного типа.
ЕО организовано в одну смену с 2100 до 500 на двух поточных линиях непрерывного действия, состоящей из трех постов каждая.
ТО-1 организовано в одну смену с 2115 до 515 на поточной линии периодического действия.
ТО-2 организовано в одну смену с 800 до 1600 на 4-х тупиковых постах канавного типа.
Д-1 организовано синхронно с ТО-1.
Д-2 организовано синхронно с ТО-2.
Работа в агрегатном цехе организована в одну смену с 800 до 1600.
Общая численность производственных рабочих:
на постах в цехах
ЕО – 30 чел. ТО-2 – 2 чел.
ТО-1 – 13 чел. ТР – 43 чел.
Д-1 – 2 чел.
ТО-2 – 15 чел.
Д-2 – 2 чел.
ТР – 33 чел.
Агрегатный цех спроектирован с учетом технологического тяготения, требований СНиП, пожарной безопасности и охраны окружающей среды.
Производственные площади объектов ПАТП рассчитаны с учетом нормативов площадей на одно рабочее место, на один пост и на один инвентарный автобус.
Площадь агрегатного цеха рассчитана с учетом коэффициента плотности расстановки оборудования и суммарной площади занимаемой оборудованием.
Агрегатный цех предприятия оснащен современным ГАРО, оснасткой, приспособлениями и инструментом.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Акбашев Т.Ф. Непрерывное образование и развивающаяся кооперация // Вестник высшей школы. – 1988. – № 10. - С. 34—38.
2. Акопов Г.В. Социальная психология образования. – Самара, 1996.
3. Алхасова И.В. Становление и перспективы развития рынка труда в России. – Кострома, 1996.
4. Атутов П.Р. Концепция политехнического образования в современных условиях // Педагогика. – 1999. – №2.
5. Ашмаров И.А. Экономические институты рынка труда. – Воронеж, 2003.
6. Байденко В.И. Диверсификация среднего профессионального образования. – М., 1995.
7. Баллер Э.А. Преемственность // Философская энциклопедия /Под ред. Ф.В. Константинова. – Т. 4. – М., 1967.
8. Баллер Э.А. Преемственность в развитии культуры. – М.: Наука, 1969.
9. Батышев С.Я. Задачи системы профессионального образования в условиях развития рыночной экономики. – М., 1993.
10. Батышев С.Я. Подготовка рабочих в средних профессионально-технических училищах. – М.: Педагогика, 1988.
11. Беспалько В.П. Основы теории педагогической системы. Проблемы и методы психолого-педагогического обеспечения технических обучающих систем. – Воронеж: Воронежский университет, 1977.
12. Беспалько В.П. Педагогика и прогрессивные технологии обучения. – М., 1995.
13. Большая Советская Энциклопедия на интернет-сайте http://www.yandex.ru
14. Васильева С.В. Интеграция содержания обучения как средство совершенствования профессиональной подготовки специалиста. – М., 1994.
15. Владиславлев А.Н. Непрерывное образование: проблемы и перспективы. – М.: Молодая гвардия. – 1978.
16. Владиславлев А.П. Непрерывное образование: проблемы и перспективы. – М., 1978.
17. Гершунский Б.С. Педагогические аспекты непрерывного образования // Вестник высшей школы. – 1987. – № 8. – С. 22-29.
Глущенко А.А. Влияние интеграции учебной и научной деятельности преподавателя высшей школы на качество подготовки специалиста. – М., 1998.
18. Годник С.М. Процесс преемственности высшей и средней школы. Воронеж: Воронежский университет, 1982.
19. Гольдин И.Н. Проблемное обучение в профессионально-технических училищах. – М.: Высшая школа, 1979.
20. Гонелинг Ш.И. О преемственности и межпредметных связях. Преемственность в обучении и взаимосвязь между учебными предметами в 5-6 классах. – М., 1961.
21. Даринский А.В. Непрерывное образование // Сов. педагогика. –1975. – № 1.
22. Жданов Р.П. Профессиональное становление специалиста среднего звена в системе непрерывного образования. – Красноярск, 1994.
23. Загвязинский В.И. Методология и методика социально-педагогического исследования. – М.: Педагогика, 1981.
24. Зеер Э.Ф. Личностно-ориентированные технологии профессионального развития специалиста /Сб. Инновационные формы и технологии в профессиональном и профессионально-педагогическом образовании. – Екатеринбург: УР ГППУ. – 1995. – С. – 17-18.
25. Ивков В.А. Система образования и формирование профессионально-квалификационной структуры рынка труда в переходной экономики России. – Кострома, 1999.
26. Интернет-сайт «Общество «Знание» России» http://www.znanie.org/obrazovanie/index.html
27. Интернет-сайт «Российское образование. Федеральный портал» http://www.edu.ru
28. Каган М.С. Человеческая деятельность. - М., 1974. - С. 328.
29. Концепция непрерывного образования // Народное образование. 1989. – № 10. – С. 3-12.
30. Кузьмина Н.В. Оценки психологии труда учителя. – М.: Изд-во ЛГУ, 1967.
31. Кузьмина Н.В. Формирование педагогических способностей. – М.: Изд-во ЛГУ, 1961.
32. Кумба Ф. Кризис образования в современном мире. – М., 1979.
33. Кустов Ю.А. Преемственность профессиональной подготовки молодежи в профтехучилище и вузах. – Саратов: Изд-во Саратовского университета, 1990.
34. Леднев В.С. Содержание образования. М., 1989.
35. Лужков С.А. Моделирование содержания непрерывного профессионального образования при подготовки специалистов морского транспорта. – М., 2001.
36. Маркова А.К. Психология профессионализма.- М., 1996.
37. Мичурина Е.С. Формирование профессионального самоопределения студентов в условиях непрерывного технического образования. – Кемерово, 1999.
38. Мороз А.Г. Пути обеспечения преемственности в самостоятельной учебной работе учащихся средней общеобразовательной школы и студентов вуза. Автореф. ... канд. дис. – Киев, 1972. – с. 10.
39. Муравьев С.Р. Особенности функционирования Российского рынка рабочей силы как результат влияния институциональных и организационных факторов. – М, 2003.
40. Мухашев З.А. Преемственность как момент развития. – Алма-Ата: Казахстан, 1980.
41. Новиков А.М. Перспективы создания системы НПО // Специалист. – 1998. .-№1,2. – С. 2-8.
42. Новиков А.М. Проблемы гуманизации профессионального образования// Педагогика, 2000. – №9. – С. 3.
43. Новиков А.М. Профессиональное образование России // Перспективы развития. – М.: НЦП НПО РАО, 1997.
44. Новиков П.Н. Теоретические основы опережающего профессионального образования.- М., 1997.
45. "Об образовании" Закон Российской Федерации в редакции Федерального закона от 13.01.96 N 12-ФЗ. Статья 23.
46. «О приоритетных направлениях развития образовательной системы Российской Федерации» /Решение Коллегии Министерства образования и науки РФ № ПК-5 от 4.11.2004.
47. О проблемах сохранения единства образовательного пространства в Российской Федерации. Министерство образования Российской Федерации. Решение коллегии от 05.12.2000 № 19 97.
48. Онушкин В.Г. Теоретические основы непрерывного образования. – М.: ВШ, 1987.
49. Онушкин В.Г., Кулюткин Ю.Н. Непрерывное образование – приоритетное направление науки // Современная педагогика. – 1989. – №2. – С. 14-19.
50. Педагогика открытости и диалога культур. Под ред. М.Н. Певзнера, В.О. Букетова, О.М. Зайченко. - М.: Исследовательский центр проблем качества подготовки специалистов, 2000.- С. 265.
51. Перспективы развития системы непрерывного образования / Под. ред. Б.С. Гершунского. – М.: Педагогика, 1991.
52. Поляков М.И. Модели и методы оценки конкурентоспособности образовательных услуг. – СПб, 2004.
53. Рахимова Г.С. Конкурентный потенциал и конкурентная стратегия в совокупности отношений конкурентоспособности. – Казань, 2003.
54. Редько Л.Л. Управление качеством непрерывного уровневого педагогического образования в условиях формирования региональных образовательных систем. – Ростов-н/Д, 2001.
55. Сафин А.И. Построение содержания НПО в системе «ПУ – лицей - колледж». - Казань, 1999.
56. Скаткин М.Л. Методология и методика педагогических исследований / В помощь начинающему исследователю. – М.: Педагогика, 1986. – 150 с.
57. Субетто А.И. Квалитология образования. - СПб.- М.: Исследовательский центр проблем качества подготовки специалистов, 2000. - С.200.
58. Федеральная целевая программа развития образования на 2006-2010 гг., утверждена Постановлением Правительства РФ 23.12.2005 г. (№ 803).
59. Филипов В.Ф. Сочетание общеобразовательной и профессиональной подготовки учащихся в условиях непрерывного профессионального образования. – М., 1996.
60. A Memorandum on Lifelong Learning, Мадрид, 2000.
61. European Council Presidency Conclusions, Лиссабон, 23-24 марта 2000.
62. ГАРО, Новгородский з-д Автоспецоборудования, Новгород, 1988.
63. Домке Э.Р., Балашкин А.Б. и др. Курсовое и дипломное проектирование. Методика и общие требования. Издательство ПГУ Пенза, 2003. – 225 с.
64. Епифанов Л.И., Епифанова Е.А. Техническое обслуживание и ремонт автомобилей. - М.: Форум – Инфра – М, 2002.
65. Карташов В.П. Технологическое проектирование АТП, изд. 2. - М.: Транспорт, 1981.
66. Крамаренко Г.В. Техническая эксплуатация автомобилей. - М.: Транспорт, 1983.
67. Краткий автомобильный справочник. - М.: НИИАТ, 1994.
68. Напольский Г.М. Технологическое проектирование автотранспортных предприятий и станций технического обслуживания. - М.: Транспорт, 1985.
69. Положение о техническом обслуживании и ремонте подвижного состава автомобильного транспорта. - М.: Транспорт, 1988.
70. Справочная книга для проектирования электрического освещения. Под ред. Г.М. Киорринга. Л.: «Энергия», 1996.
71. Суханов Б.Н. и др. Техническое обслуживание и ремонт автомобилей: Пособие по дипломному проектированию. - М.: Транспорт, 1991.