Контрольная работа: Расчет балки

Задача №1.

привод крутящий момент балка

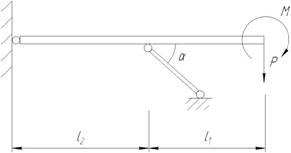
Р = 13 кН, М = 9 кН·м,

l1 = 0,9 м, l2 = 1,1 м,

α = 30°.

RA – ? NA – ? RB – ?

Решение

Составим расчетную схему балки, опоры заменим реакциями опор (рис. 1).

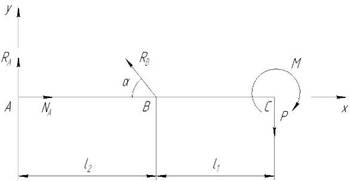
Рис. 1

Составим уравнение моментов относительно точки А:

ΣМ(А) = RB·sinα·l2 – M – P(l1 + l2) = 0;

Составим уравнение моментов относительно точки B:

ΣМ(B) = – RA·l2 – M – P·l1 = 0;

Проверка:

ΣFY = RB·sinα + RA – P = 0;

63,6·sin30° – 18,8 – 13 = 0;

0 = 0 – реакции найдены верно.

Составим уравнение сил по оси х:

ΣFХ = NA – RB·cosα = 0;

NA = RB·cosα = 63,6·cos30° = 55,1 кH.

Реакции опорного шарнира: RA и NA.

Сила, нагружающая стержень по модулю равна RB и направлена в противоположную сторону.

Задача №2.

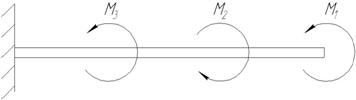
М1 = 440 Н·м, М2 = 200 Н·м,

М3 = 860 Н·м, [τ]кр = 100 МПа,

Ст3, круг, кольцо d0/d = 0,7

d кр – ? d0 – ? d – ?

Решение

Для заданного бруса построим эпюру крутящих моментов (рис. 2).

Заданный брус имеет три участка нагружения.

Возьмем произвольное сечение в пределах I участка и отбросим левую часть бруса.

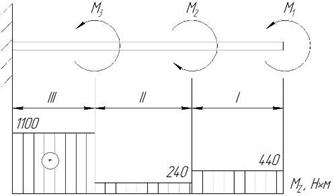
Рис. 2

На оставленную часть бруса действуют моменты М1 и МZI. Следовательно:

МZI = М1 = 440 Н∙м.

Взяв произвольное сечение в пределах II участка, и рассматривая равновесие оставленной части бруса получим:

МZII = М1 – M2 = 440 – 200 = 240 Н∙м.

Взяв произвольное сечение в пределах III участка, и рассматривая равновесие оставленной части бруса получим:

МZIII = М1 – M2 + M3 = 440 – 200 +860 = 1100 Н∙м.

По имеющимся данным строим эпюру крутящих моментов.

Условие прочности:

Отсюда:

Для круга:

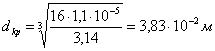
Для кольца:

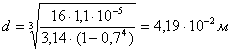
Массы брусьев.

Круг.

Кольцо.

Так как S2 < S1, то масса бруса с сечением в форме круга больше, чем с сечением в форме кольца.

Увеличим размер сечения в два раза.

Рассмотрим круг.

При увеличении размера сечения круга в 2 раза, нагрузку на брус можно увеличить в 8 раз.

Затраты материала увеличатся в 4 раза.

Аналогично получаются такие же результаты для сечения в форме кольца, так как формулы схожи.

Задача №3.

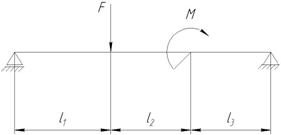
F = 21 кН, М = 13 кН·м,

l1 = 0,9 м, [δ]изг = 150 МПа,

l2 = 0,5 м, l3 = 0,7 м,

Ст3, швеллер, прямоугольник

h/b = 3

швеллер – ? h – ? b – ?

Решение

Отбросив опоры, заменим их действие на балку реакциями RA и RВ. Определим значение RA и RВ.

ΣМА(Fi) = F·l1 + M – RВ (l1 + l2 + l3) = 0;

ΣМB(Fi) = – F·(l2 +l3) + M + RA (l1 + l2 + l3) = 0;

Проверка:

ΣFi = RB + RA – F = 0;

15,2 + 5,8 – 21 = 0;

0 = 0 – реакции найдены верно.

Балка имеет три участка нагружения.

Возьмем произвольное сечение в пределах I участка:

QyI = RA = 5,8 кН

МХI = RA∙z

При z = 0; МХI(0) = 0.

При z = l1; МХI(0,9) = 5,8∙0,9 = 5,2 кН∙м.

Возьмем произвольное сечение в пределах II участка:

QyII = RA – F = 5,8 – 21 = -15,2 кН

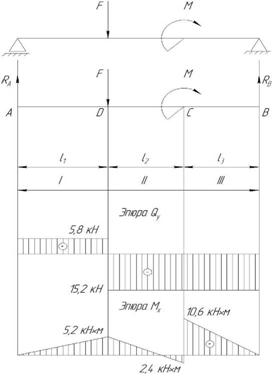
Рис. 3

МХII = RA∙z – F (z – l1)

При z = l1 + l2; МХII(1,4) = 5,8∙1,4 – 21∙0,5 = -2,4 кН∙м.

В точке, расположенной бесконечно близко справа от точки С:

МХII’ = RA∙z – F (z – l1) + M

МХII’ (1,4) = 5,8∙1,4 – 21∙0,5 + 13 = 10,6 кН∙м.

Возьмем произвольное сечение в пределах III участка:

QyIII = RA – F = 5,8 – 21 = -15,2 кН

МХIII = RA∙z – F (z – l1) + M

В точке В: МХIII = 0.

По имеющимся данным строим эпюры поперечных сил и изгибающих моментов (рис. 3).

Условие прочности:

Отсюда:

Швеллер.

Берем швеллер №14а с WX = 77,8 см3, SX = 45,1 см3 = 4,51∙10-5 м3.

Прямоугольник.

Так как SХ < S, то масса балки с сечением в форме прямоугольника больше, чем масса балки из швеллера.

Увеличим размеры прямоугольного сечения в два раза.

- затраты материала увеличатся в два раза.

- нагрузку можно увеличить в два раза.

- затраты материала увеличатся в два раза.

- нагрузку можно увеличить в четыре раза.

Задача №4

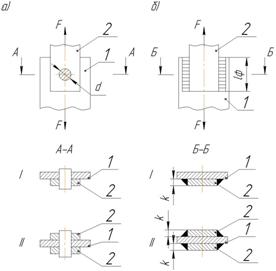
lф = 100 мм, [τ]ср = 80 МПа,

k = 6 мм, [τ]’ср = 100 МПа.

d – ?

Решение

Найдем силу F из условия прочности швов при срезе.

I схема.

F = 0,7·[τ]’ср ·k·2·lф = 0,7·100·106·0,006·2·0,1 = 84 кН

II схема.

F = 0,7·[τ]’ср ·k·4·lф = 0,7·100·106·0,006·4·0,1 = 168 кН

Условие прочности на срез:

Определим диаметр пальца из условия прочности при срезе.

I схема.

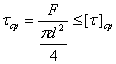
Берем d = 37 мм.

II схема.

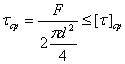
Берем d = 37 мм.

Задача №5.

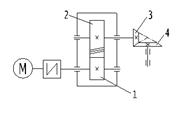
Рдв = 4 кВт, ωдв = 158 рад/с, Z3 = 24, Z4 = 36, ωвых = 38 рад/с, ηц = 0,97, ηк = 0,95,

а = 140 мм, ψ = 0,5.

ηобщ – ? Uобщ – ? Рi – ? Mi – ?

Решение

Общий КПД привода:

ηобщ = ηц · ηк · ηм · ηп3

ηц. – КПД зубчатой цилиндрической передачи;

ηк. – КПД зубчатой конической передачи;

ηм = 0,98 – КПД муфты;

ηп = 0,98…0,99; принимаем ηп = 0,98 – КПД пары подшипников качения.

ηобщ = 0,97 · 0,95 · 0,98 · 0,983 = 0,85

Общее передаточное отношение привода:

Uобщ = ωдв / ωвых = 158 / 38 = 4,16

Передаточное отношение конической передачи:

Uк = Z4 / Z3= 36 / 24 = 1,5

Передаточное отношение цилиндрической передачи:

Uц = Uобщ / Uк = 4,16 / 1,5 = 2,77

Вал двигателя.

Рдв = 4 кВт;

ωдв = 158 рад/с;

Тдв = Рдв / ωдв = 4000 / 158 = 25,32 Н·м.

Быстроходный вал редуктора.

Р1 = Рдв · ηм · ηп = 4 · 0,98 · 0,98 = 3,84 кВт;

ω1 = ωдв = 158 рад/с;

Т1 = Тдв · ηм · ηп = 25,32 · 0,98 · 0,98 = 24,32 Н·м.

Тихоходный вал редуктора.

Р2 = Р1 · ηп · ηц = 3,84 · 0,98 · 0,97 = 3,65 кВт;

ω2 = ω1 / Uц = 158 / 2,77 = 57,04 рад/с;

Т2 = Т1 · Uц · ηц. · ηп = 24,32 · 2,77 · 0,98 · 0,97 = 64,04 Н·м.

Выходной вал привода.

Р3 = Р2 · ηп · ηк = 3,65 · 0,98 · 0,95 = 3,4 кВт;

ωвых = 38 рад/с;

Т3 = Т2 · Uк · ηк. · ηп = 64,04 · 1,5 · 0,98 · 0,95 = 89,43 Н·м.

Данный привод имеет две ступени. Первая ступень – косозубый цилиндрический редуктор. Вторая ступень – открытая коническая передача. Электродвигатель соединен с быстроходным валом редуктора муфтой. Основные технические характеристики привода:

· КПД – 0,85;

· Общее передаточное число – 4,16;

· Вращающий момент на выходном валу – 89,43 Н·м;

· Угловая скорость выходного вала – 38 рад/с.

Цилиндрические колеса, у которых зубья расположены по винтовым линиям на делительном диаметре, называют косозубыми. При работе такой передачи зубья входят в зацепление не сразу по всей длине, как в прямозубой, а постепенно; передаваемая нагрузка распределяется на несколько зубьев. В результате по сравнению с прямозубой повышается нагрузочная способность, увеличивается плавность работы передачи и уменьшается шум. В целом, косозубые колёса применяются в механизмах, требующих передачи большого крутящего момента на высоких скоростях, либо имеющих жёсткие ограничения по шумности.

Недостатками косозубых колёс можно считать следующие факторы:

При работе косозубого колеса возникает механическая сила, направленная вдоль оси, что вызывает необходимость применения для установки вала упорных подшипников;

Увеличение площади трения зубьев (что вызывает дополнительные потери мощности на нагрев), которое компенсируется применением специальных смазок.

Основные формулы для расчета косозубой передачи приведены ниже.

Конические зубчатые колеса применяют в передачах, у которых оси валов пересекаются под некоторым углом. Наиболее распространены передачи с углом 90°.

Аналогами начальных и делительных цилиндров цилиндрических передач в конических передачах являются начальные и делительные конусы с углами δ1 и δ2.

При коэффициентах смещения инструмента х1 + х2 = 0 начальные и делительные конусы совпадают. Конусы, образующие которых перпендикулярны образующим елительных конусов, называют дополнительными конусами. Сечение зубьев дополнительным конусом называют торцовым сечением. Различают внешнее, внутреннее и среднее торцовые сечения.

Основными габаритными размерами для конических передач являются de2 и Re, а нагрузка характеризуется моментом Т2 на ведомом валу. Основные зависимости:

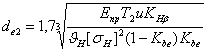d’m1 = d’e1(R’e – 0,5b’)/R’e,

m’nm = m’tmcosβn,

dm1 = mtmz1, dm2 = mtmz2.

Из различных типов конических колес с непрямыми зубьями на практике получили распространение колеса с косыми или тангенциальными зубьями и колеса с круговыми зубьями. Преимущественное применение получили колеса с круговыми зубьями. Они менее чувствительны к нарушению точности взаимного расположения колес, их изготовление проще.

Конические передачи применяются при пересекающихся валах. Конические передачи дорогие. Выгодны не прямозубые, а косозубые колеса, так как они позволяют уменьшить габариты и массу.

Выполним геометрический расчет передачи редуктора.

Модуль зацепления:

m = (0,01–0,02) α = 1,4 – 2,8 мм, принимаем m = 2 мм.

Ширина колеса:

b2 = ψ · α = 0,5 · 140 = 70 мм

b1 = b2 + 5 = 70 + 5 = 75 мм – ширина шестерни.

Минимальный угол наклона зубьев:

βmin = arcsin = arcsin = 5,7°

При β = βmin сумма чисел зубьев zc = z1 + z2 = (2α/m) cos βmin = (2 · 140/2) cos 5,7°= 139,3

Округляем до целого: zc = 139

Угол наклона зубьев:

β = arccos = arccos = 6,85°,

при нем zc = (2 · 140/2) cos 6,85° = 139

Число зубьев шестерни:

z1 = zc / (Uц + 1) = 139 / (2,77 + 1) ≈ 37

z2 = 139 – 37 = 102 – колеса.

Передаточное число:

Uф = 102 / 37 = 2,76, отклонение ΔU = 0,02U – допустимо.

Диаметры делительных окружностей:

d1 = m z1 /cos β = 2 · 37 / cos 6,85° = 74,5 мм – шестерни;

d2 = m z2 /cos β = 2 · 102 / cos 6,85° = 205,5 мм – колеса.

Торцевой (окружной) модуль:

mt = m /cos β = 2 / cos 6,85° = 2,014

Диаметры вершин зубьев:

dа1 = d1 + 2m = 74,5 + 2 · 2 = 78,5 мм;

dа2 = d2 + 2m = 205,5 + 2 · 2 = 209,5 мм.

Диаметры впадин зубьев:

df1 = d1 - 2,5m = 74,5 – 2,5 · 2 = 69,5 мм;

df2 = d2 - 2,5m = 205,5 – 2,5 · 2 = 200,5 мм.