
Главная
Рефераты по зарубежной литературе
Рефераты по логике
Рефераты по маркетингу
Рефераты по международному публичному праву
Рефераты по международному частному праву
Рефераты по международным отношениям
Рефераты по культуре и искусству
Рефераты по менеджменту
Рефераты по металлургии
Рефераты по муниципальному праву
Рефераты по налогообложению
Рефераты по оккультизму и уфологии
Рефераты по педагогике
Рефераты по политологии
Рефераты по праву
Биографии
Рефераты по предпринимательству
Рефераты по психологии
Рефераты по радиоэлектронике
Рефераты по риторике
Рефераты по социологии
Рефераты по статистике
Рефераты по страхованию
Рефераты по строительству
Рефераты по схемотехнике
Рефераты по таможенной системе
Сочинения по литературе и русскому языку
Рефераты по теории государства и права
Рефераты по теории организации
Рефераты по теплотехнике
Рефераты по технологии
Рефераты по товароведению
Рефераты по транспорту
Рефераты по трудовому праву
Рефераты по туризму
Рефераты по уголовному праву и процессу
Рефераты по управлению
Курсовая работа: Розрахунок монолітного залізобетонного акведука
Курсовая работа: Розрахунок монолітного залізобетонного акведука
Міністерство освіти і науки України
Кафедра інженерних конструкцій
Курсовий проект
на тему:
«Розрахунок монолітного залізобетонного акведука»
Рівне 2004
Зміст
1. Визначення основних розмірів конструкцій
1.1 Лотік
1.2 Прольоти другорядних балок і виліт консолей
1.3 Поперечні перерізи основних несучих елементів
2. Розрахунок і конструювання лотока
2.1 Визначення навантажень на лотік
2.2 Визначення зусиль у перерізах лотока
2.3 Розрахунок міцності нормальних перерізів лотока
2.4 Розрахунок міцності похилих перерізів плити лотока
2.5 Розрахунок плити лотока на розкриття тріщин
2.6 Конструювання лотока
3. Розрахунок і конструювання другорядної балки
3.1 Визначення навантажень на балку
3.2 Визначення зусиль у перерізах другорядної балки
3.3 Розрахунок міцності нормальних перерізів другорядної балки
3.4 Розрахунок міцності похилих перерізів другорядної балки
3.5 Конструювання балки. Побудова епюри матеріалів
4. Розрахунок рами акведука
4.1 Статичний розрахунок рами
4.2 Розрахунок ригеля рами
4.2.1 Розрахунок міцності нормальних перерізів ригеля
4.2.2 Розрахунок міцності похилих перерізів ригеля
4.2.3 Розрахунок на відрив
4.3 Розрахунок і конструювання колони
5. Розрахунок фундаменту
5.1 Визначення розмірів підошви фундаменту
5.2 Визначення необхідної висоти фундаменту
5.3 Призначення розмірів уступів фундаменту
5.4 Розрахунок робочої арматури фундаменту
Література
1. Визначення основних розмірів конструкцій
1.1 Лоток
Товщину дна і стінок лотока визначаємо за більшим з двох значень, приймаючи її кратною 10 мм:
![]() ;
;
![]() .
.
Приймаємо
![]() .
.
Висоту стінок призначаємо на 20 см вище рівня води
![]()
У місцях з’єднання дна та стінок лотока влаштовуємо скоси (вути) висотою 10 см під кутом 450.
1.2 Прольоти другорядних балок і виліт консолей
Загальну довжину моста – водоводу L визначаємо за формулою
![]() ,
,
де ![]() – проліт
другорядних балок, який приймають в межах (5... 8) м;
– проліт
другорядних балок, який приймають в межах (5... 8) м;
![]() – довжина
консолей;
– довжина
консолей;
![]() – кількість
прольотів другорядних балок;
– кількість
прольотів другорядних балок;
![]() , приймаємо
значення с=0,4.
, приймаємо
значення с=0,4.
Визначаємо значення прольоту другорядних балок
![]() .
.
Виліт консолі
![]() .
.
Приймаємо lb = 6,2 м, lc = 2,5 м.
1.3 Поперечні перерізи основних несучих елементів
Задаємо висоту другорядних балок
![]() ;
;
висоту ригелів
![]()
Ширину
другорядних балок ![]() і ригелів
і ригелів ![]() вибираємо у межах:
вибираємо у межах:
![]() ;
;
![]() .
.
Приймаємо
![]() ,
,![]() ;
; ![]() .
.
Розміри поперечного перерізу стояка рами призначаємо
![]() ;
;
![]() ,
,
де Н – висота колони, яку приймають рівною віддалі від осі ригеля до верху фундаменту,
![]() .
.
Висоту фундаменту приймаємо hf = 80 cм.
Поздовжній та поперечний розрізи акведука за прийнятими даними поданий на рис. 1.1.
2. Розрахунок і конструювання лотока
2.1 Визначення навантажень на лотік
Розрахункова схема лотока у поперечному напрямку – нерозрізна плита балочного типу, опорами якої є другорядні балки, завантажена власною вагою та тиском води, з розрахунковим прольотом, рівним відстані між внутрішніми гранями другорядних балок.
Для зручності розрахунку стінки лотока умовно розміщуємо у горизонтальному положенні (рис. 2.1).
Розрахункові навантаження на 1 погонний метр плити шириною 1 м визначаємо за формулами:
навантаження від тиску води
![]() ;
;
навантаження від маси дна лотока
gm = g · (ρb · hs · γ fb+ ρsc · hsc · γfc) = 10 · (2500 · 0,18 · 1,05 + 1800 · 0,02 ·1,2) = 5157 Н/м = 5,16 кН/м,
де ρw = 1000 кг/м3; ρb = 2500 кг/м3; ρsc = 1800 кг/м3 – густина, відповідно води, залізобетону, торкрет-штукатурки;
γfw = 1,0; γfb = 1,05; γfc = 1,2 – коефіцієнти надійності за навантаженням відповідно для води, залізобетону і торкрет-штукатурки;
g – прискорення земного тяжіння (g = 10 м/с2).
Повне розрахункове навантаження
q = gm + gw = 17+5,16 = 22,16 кН/м.
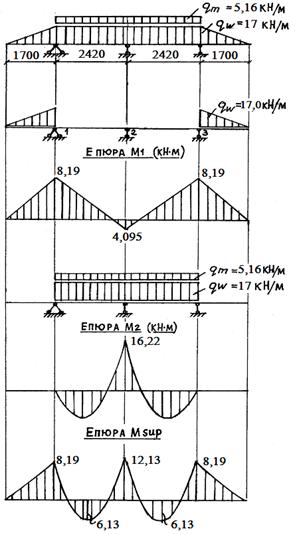
2.2 Визначення зусиль у перерізах лотока
Розрахункова схема лотока, з точки зору статики – два рази статично невизначена балка. У поперечному напрямку являє собою плиту, опорами для якої служать другорядні балки.
|
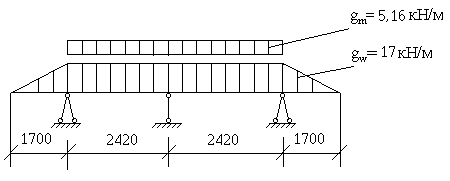
lsc= hw=1,7 м; lef = ls – bb=2,6 – 0,18=2,42 м.
Для зручності розрахунків розрахункову схему (рис. 2.1) розділимо на дві: завантаження тільки на консолях (рис.2.2,б) і завантаження у прольоті (рис.2.2,г).
Значення згинаючих моментів у опорних перерізах лотока визначимо, використовуючи табличні коефіцієнти (додатки 1,2 [2]), тоді зручно дію навантажень на консолі замінити моментом Мс, який прикладений на крайніх опорах
Mc =gw · hw2 / 6=17 ·1,72 /6=8,19 кН·м.
Опорні моменти :
за першою схемою завантаження
М11 = М31 = к1 · Мс = (–1) · 8,19 = – 8,19 кН·м;
М21 = к2 · Мс = 0,5 · 8,19 = 4,095 кН·м;
за другою схемою завантаження
М12 = М32 = 0; М22 = α2 · q · lef 2 = – 0,125 · 22,16 · 2,422 = – 16,22 кН·м;
Значення опорних моментів (Мsup) за розрахунковою схемою (рис. 3.2, а) отримаємо методом алгебраїчного складування:
![]() ;
; ![]() .
.
Значення максимальних прольотних моментів визначимо, вирізаючи кожний проліт і прикладаючи навантаження у ньому та опорні моменти.
Проліт 1-2
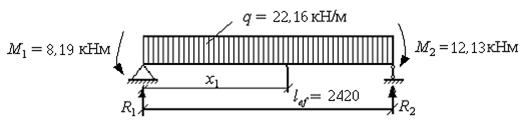
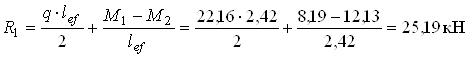 ;
;
R2 = (q · lef) – R1 = (22,16 · 2,42) – 25,19 = 28,44 кН.
Відстань від лівої опори до нульової точки епюри поперечних сил
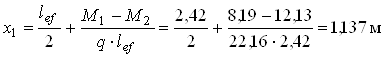 .
.
Максимальний пролітний момент
M1 – 2
= R1 · x1 – ![]() –
M1 = 25,19 · 1,137 –
–
M1 = 25,19 · 1,137 – ![]() – 8,19 = 6,13 кН·м.
– 8,19 = 6,13 кН·м.
|
2.3 Розрахунок міцності нормальних перерізів лотока
Розрахунками міцності лотока за нормальними перерізами визначаємо площу поперечного перерізу арматури в прольотах і на опорах, як для згинальних елементів прямокутного перерізу шириною bs = 100 см і висотою
hs = 17 см.
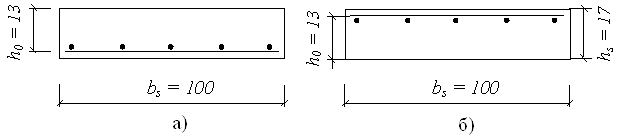 Рис.2.3. Розрахункові
перерізи плити лотока а) в прольоті; б) на опорі
Рис.2.3. Розрахункові
перерізи плити лотока а) в прольоті; б) на опорі
За розрахунковий переріз приймаємо прямокутний з розмірами
![]() ,
,
де h0
= hs – a = 17 – 4 = 13 см; а – товщина захисного шару бетону (для плити лотока
приймаємо ![]() );
);
Матеріали лотока:
– бетон класу В20 – Rb =11,5 МПа; Rbt = 0,9 МПа; Es = 3,0 · 10 4 МПа;
– арматура класу А-ІІI – Rs =355 МПа; Es = 2 ·105 МПа (табл. 7.3; 7.5; 7.9 і 7.11 [5]).
Значення коефіцієнтів :
γlc = 1,0 - коефіцієнт сполучення навантажень;
γn = 1,15 - коефіцієнт надійності за призначенням споруд;
γb3 = 1,1 - коефіцієнт умов роботи бетону [6];
γs2 = 1,1 - коефіцієнт умов роботи арматури [6].
Визначимо потрібну площу перерізу арматури на опорах і в прольотах за відповідними згинаючими моментами.
Опора 1. М1 = 8,19 кН·м = 819 кН·см.
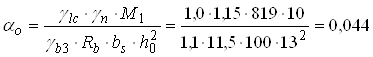 .
.
За табл. додатку 5 [2] за α0 = 0,044 знаходимо значення коефіцієнтів η=0,978; ξ = 0,045. Для бетону класу В20 і арматури класу А-ІІІ граничне значення відносної висоти стиснутої зони бетону ξR = 0,6 (додаток 8 [2]).
Так як ξ = 0,045 < ξR = 0,6, стиснута арматура за розрахунком не потрібна.
Потрібна площа перерізу розтягнутої арматури
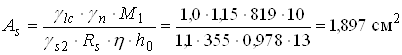 .
.
Приймаємо 5 Æ 7 А-ІІІ, (As = 1,92 см2, додаток 6 [2], табл. 5.41[5]).
Процент армування
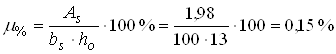 ,
,
що
більше мінімального проценту армування для згинальних елементів ![]() (табл. 7.28 [5]).
(табл. 7.28 [5]).
Для інших перерізів арматура підібрана аналогічно і прийнята:
на опорі 2, 6Æ 8 А-ІІІ (А = 3,02 см2);
в прольотах 1 – 2, 2 – 3, 5Æ 6 А-ІІІ (А = 1,42 см2).
2.4 Розрахунок міцності похилих перерізів плити лотока
Розрахунок на міцність похилих перерізів плити можна не виконувати за дотримання умови
![]() ,
,
де Q
= 28,44 кН – максимальна поперечна сила у плиті лотока ![]() ;
;
Qb – поперечне зусилля, яке сприймає бетон стиснутої зони в похилому перерізі і визначене за формулою
Qb = φ2 · Rbt · bs ·ho · tgβ,
де φ2 = 0,5 + 2μ · Rs / Rb = 0,5 + 2 · 0,0023 · 355 / 11,5 = 0,642;
![]() , (As = 3,02 см2
на опорі 2);
, (As = 3,02 см2
на опорі 2);
Приймемо tgβ = 0,5.
Qb = 0,642 · 0,9 · 100 · 13 · 0,5 · 100 = 75114 H = 37,56 кH.
1,0 · 1,15 · 28,44 кН = 32,71 кН < 1,1 · 37,56 = 41,31 кН.
Умова виконується. Міцність похилих перерізів забезпечена.
2.5 Конструювання лотока
Армування стін і дна лотока здійснюємо зварними сітками. Стіни з внутрішнього боку армують відповідно до виконаних розрахунків на міцність і тріщиностійкість за дії згинаючих моментів, а із зовнішнього боку – за конструктивними вимогами дотримання мінімального проценту армування, тобто Аs = 0,0005 · b · ho.
У плиті днища лотока прольотну і надопорну арматуру влаштовуємо згідно розрахунків. Крайні прольоти армуємо подвійною арматурою, тому що в цих місцях крім згинаючих моментів виникають розтягуючі зусилля від дії води на стінки лотока. Розподільчу арматуру призначаємо конструктивно із сталі класу Вр-І з кроком 250...300 мм (кратно 50 мм).
3. Розрахунок і конструювання другорядної балки
3.1 Визначення навантажень на балку
Розрахунку підлягає одна із середніх балок, як найбільш навантажена. Розрахункова схема другорядної балки акведука являє собою багатопролітну нерозрізну балку з двома консолями, опорами для якої є ригелі поперечних рам, завантажену рівномірним навантаженням від власної ваги, ваги плити лотока та води (рис. 3.1).
Розрахункові прольоти і консолі балки
lefb = lb – lmb = 6,2 – 0,2 = 6,0 м; lscb = ls – 0,5bmb = 2,5 – 0,5 · 0,2 =2,4 м.
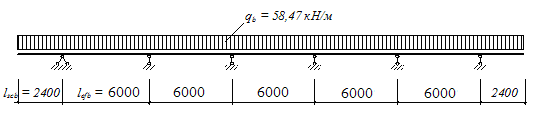
Рис. 3.1. Розрахункова схема другорядної балки
Повне навантаження qb на 1 м довжини середньої другорядної балки обчислюємо за формулою
qb = ls · q + g · ρb· bb · h1 · γfb,
де q – повне навантаження на дно лотока;
bb – ширина другорядної балки;
ls – відстань між осями другорядних балок;
h1 – висота балки, яку для акведука із монолітного залізобетону приймають
h1 = hb – hs = 35 –17 = 18 см,
qb = 2,6 · 22,16 + 10 · 2,5 · 0,18 · 0,18 · 1,05 = 58,47 кН/м.
3.2 Визначення зусиль у перерізах другорядної балки
Значення згинаючих моментів та поперечних сил в балках визначаємо з використанням табличних коефіцієнтів, які наведені в додатках 1 і 2 [2].
Користуючись наведеними табличними коефіцієнтами, необхідно дію навантажень на консолі замінити відповідними консольними моментами, рівними
Mc = 0,5 · qb · lscb 2.
Опорні моменти у перерізах другорядної балки визначаємо від дії консольного моменту і рівномірно розподіленого навантаження.
Опорні моменти за першою схемою завантаження (рис. 3.2, б):
М11 = М61 = 0,5 · qb ·k1· lscb2 = 0,5 · 58,47 · (– 1) · 2,42 = -168,39 кН·м;
М21= М51 = 0,5 ·qb ·k2 ·lscb2 = 0,5 · 58,47 · 0,263 · 2,42 = 44,29 кН·м;
М31= М41 = 0,5 ·qb ·k3 ·lscb2 = 0,5 · 58,47 · (-0,051) · 2,42 = - 8,59 кН·м.
Моменти за другою схемою завантаження (рис. 3.2, г):
М12 = М62 = 0;
М22 = М52 = α2 · qb · lefb2 = (-0,105) · 58,47 · 6,02 = -221,02 кН·м;
М32 = М42 = α3 · qb · lefb2 = (-0,08) · 58,47 · 6,02 = -168,39 кН·м.
Опорні моменти за повного навантаження отримуємо шляхом алгебраїчного сумування опорних моментів за двома схемами.
Для визначення прольотних моментів розглядаємо рівновагу однопролітних балочок, завантажених прольотним навантаженням і опорними моментами.
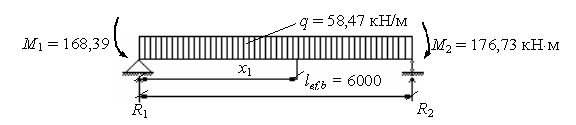 |
Перший проліт
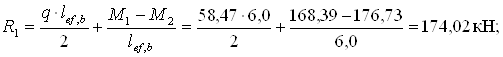
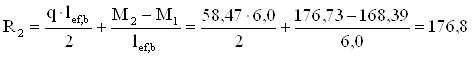 кН.
кН.
Відстань від лівої опори до нульової точки епюри поперечних сил
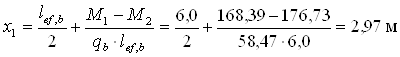
Максимальний пролітний момент
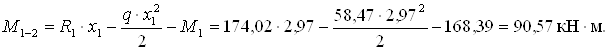
Для більш точної побудови епюри обчислюємо значення моментів через 0,2l від внутрішньої грані лівого ригеля
х01 =0,2·lef,b=0,2× 6,0=1,2 м; M01=174,02× 1,2-58,47× 1,22/2-168,39=-1,66кH×м;
x02 =0,4·lef,b=0,4· 6,0=2,4 м; M02=174,02× 2,4-58,47× 2,42/2-168,39= 80,86кH×м;
x03 =0,6·lef,b=0,6· 6,0=3,6 м; M03=174,02× 3,6-58,47× 3,62/2-168,39= 79,20кH×м;
x04 =0,8·lef,b=0,8· 6,0=4,8 м; M04=174,02× 4,8-58,47× 4,82/2-168,39= -6,67кH×м.
Другий проліт (обчислення аналогічні)
![]() = 175,37 кН; R3
= 175,45 кН; x2 = 2,999 м; M2-3 = 86,26 кН·м;
= 175,37 кН; R3
= 175,45 кН; x2 = 2,999 м; M2-3 = 86,26 кН·м;
х01 =0,2·lef,b=0,2× 6,0=1,2 м; M01= -8,39кH×м;
x02 =0,4·lef,b=0,4· 6,0=2,4 м; M02= 75,76кH×м;
x03 =0,6·lef,b=0,6· 6,0=3,6 м; M03= 75,71кH×м;
x04 =0,8·lef,b=0,8· 6,0=4,8 м; M04= -8,54кH×м.
Третій проліт (обчислення аналогічні)
![]() = R4 = 175,41
кН; x2 = 3,0 м; M2-3 = 86,14 кН·м;
= R4 = 175,41
кН; x2 = 3,0 м; M2-3 = 86,14 кН·м;
х01 =0,2·lef,b=0,2× 6,0=1,2 м; M01= -8,59кH×м;
x02 =0,4·lef,b=0,4· 6,0=2,4 м; M02= 75,61кH×м;
x03 =0,6·lef,b=0,6· 6,0=3,6 м; M03= 75,61кH×м;
x04 =0,8·lef,b=0,8· 6,0=4,8 м; M04= -8,59кH×м.
3.3 Розрахунок міцності нормальних перерізів другорядної балки
Визначаємо мінімально допустиму висоту другорядної балки за найбільшим згинаючим моментом (опорним). Значення граничної відносної висоти стиснутої зони ξR = 0,6 визначили за додатком 8 [2]. Йому відповідає значення αR = 0,42. Тоді
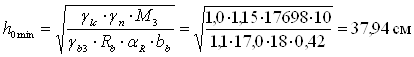 .
.
Повна мінімальна висота перерізу балки
hbmin = h0min + tb + 0,5 · d = 37,94 + 3 + 0,5 · 2 = 41,94 см.
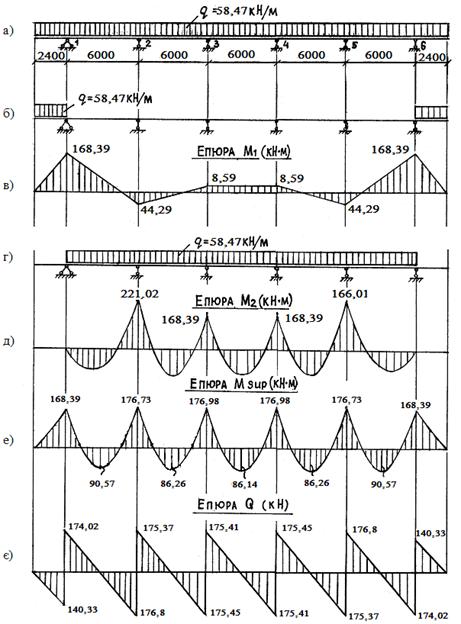 |
Рис 3.2. Розрахункова схема і епюри зусиль другорядної балки
Приймаємо розміри перерізу балки 45х18 см.
Розміри поперечного перерізу балки повинні задовільняти умову, що забезпечує необхідну міцність стиснутої зони бетону в похилих перерізах
![]()
![]() кН.
кН.
Отже умова виконується, міцність забезпечена.
Робоча висота опорних перерізів визначається з урахуванням розміщення робочої арматури другорядної балки в два ряди по висоті перерізу
h0 =
hb – tb – d – ![]() = 45 – 3 – 2 –
= 45 – 3 – 2 – ![]() = 38,5 см.
= 38,5 см.
Матеріали для другорядної балки:
бетон класу В30 – Rb = 17,0 МПа; Rbt =1,20 МПа; Eb = 3,5 · 104 МПа (табл. 7.3 і 7.5 [5]);
 |
робоча арматура класу А-ІІ – Rs= 280 МПа; Es=2,1·105 МПа (табл. 7.8 і 7.11 [5]).
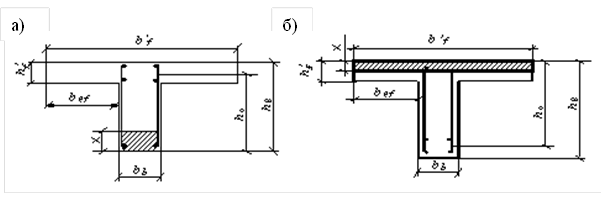
Рис. 3.3. Розрахункові перерізи балки:
а) на опорі; б) в прольоті.
Виконуємо розрахунок опорних перерізів.
Опора 1, М1 = 168,39 кН·м = 16839 кН·см.
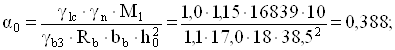 α0 =0,388
< αR = 0,42.
α0 =0,388
< αR = 0,42.
Значенню α0 =0,388 відповідає η = 0,737 x=0,527 (додаток 5 [2], табл. 7.17[5]).
Потрібна площа перерізу арматури
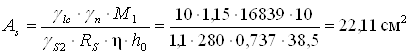 .
.
Приймаємо 2Æ28 + 2Æ25 А-ІІ, As= 22,14 см2.
Опори 2,3, М3=176,98 кН·м=17698 кН·см. α0=0,408; η=0,715; As=24,02 см2. Прийнята арматура 4Æ28 А-ІІ, As = 24,63 см2.
Розрахунковий переріз другорядної балки в прольотах, де полиця буде стиснута, залежить від положення нейтральної лінії.
Визначаємо ширину полиці bf /, що вводиться в розрахунок
![]() = 2bef + bb = 2
· 103 +18 = 224 см,
= 2bef + bb = 2
· 103 +18 = 224 см,
де bef
£ 1 / 6 · lb = 1 / 6 · 620 = 103,3 см; ![]() ,
,
у
розрахунок приймаємо менше з двох значень ![]() .
.
Визначаємо випадок розташування нейтральної лінії за умовою
![]() .
.
Значення згинаючого моменту, який може сприйняти балка за умови, що межа стиснутої зони проходить по нижній грані полички, обчислюємо за формулою
Mf = γb3 · Rb · bf ¢ · hf¢ · (h0 – 0,5 hf¢) = 1,1 · 17,0 · 224 · 17 (38,5 – 0,5 · 17) /10 = 213628,8 кН ·см = 2136,29 кН ·м,
де ![]() .
.
Оскільки Mf =2136,29 кН·м > M1-2=90,57 кН·м, нейтральна лінія проходить у поличці, а розрахунковий переріз балки прямокутний з розмірами bf´h0=224´38,5см.
Перший проліт
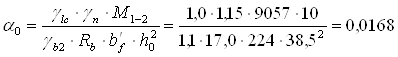
за α0 знаходимо η=0,992; x=0,0169 (табл. 7.17 [5], додаток 5[2]).
Потрібна площа арматури
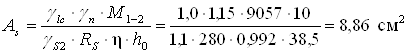 .
.
Приймаємо 2Æ18 + 2Æ16 А-ІІ, As = 9,11 см2.
Другий і третій прольоти (обчислення аналогічні)
М2-3 = 86,26 кН·м = 8626 кН·см. α0 =0,0160; η = 0,992; As = 8,43см2. Прийнята арматура 2Æ18 + 2Æ16 А-ІІ, As = 9,11 см2.
3.4 Розрахунок міцності похилих перерізів другорядної балки
Поперечну арматуру приймаємо Æ 12 мм класу А-І. Згідно конструктивних вимог, максимальний крок поперечної арматури на приопорних ділянках
Sw ![]() hb / 2 = 45/2
= 22,5 см, але не більше Sw = 15 см. Приймаємо Sw = 15 см.
hb / 2 = 45/2
= 22,5 см, але не більше Sw = 15 см. Приймаємо Sw = 15 см.
Розрахункова поперечна сила Q2 = 176,8 кН.
Визначимо мінімальну поперечну силу, яку може сприйняти бетон
Qb,min = 0,6 ·(1 + φf + φn) · Rbt · bb · h0 · γb3
Qb,min = 0,6(1 + 0 + 0) · 1,2 · 18 · 38,5 · 1,1 · 10-1 = 54,9 кН,
де φf = 0 – для прямокутного перерізу;
φn = 0 – коефіцієнт, який враховує поздовжню силу.
Так як Qb,min=54,9 кН<Q=176,8 кН, то необхідний розрахунок поперечної арматури. Мінімальне погонне зусилля у поперечній арматурі
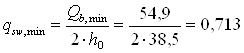 кН /см.
кН /см.
Погонне зусилля, яке може сприйняти поперечна арматура
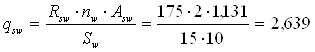 кН/см >
qsw,min = 0,713 кН /см.
кН/см >
qsw,min = 0,713 кН /см.
Проекція тріщини на вісь балки
 =
=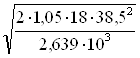 = 49,26 см
< 2 · h0 = 77 см,
= 49,26 см
< 2 · h0 = 77 см,
де φb2 = 2 – для важкого бетону.
Поперечна сила, яку сприймають бетон і поперечна арматура
Q = Qb,min + qsw · c0 = 54,9 + 2,639 · 49,26 = 184,9 > Q = 176,8 кН.
Міцність похилого перерізу на дію поперечної сили забезпечена.
Перевіряємо міцність стиснутої смуги бетону за умовою (60) [6]:
![]() ,
,
де 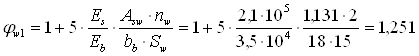 ;
;
φb1 = 1 – β · Rb = 1 – 0,01 · 17,0 = 0,83;
β = 0,01 – для важкого бетону.
176,8 кН < 0,3 · 1,251 · 0,83 · 17,0 · 10-1 · 18 · 38,5 = 366,98 кН.
3.5 Конструювання балки. Побудова епюри матеріалів
Площа арматури в балках на опорах і в прольотах визначалась за найбільшими згинаючими моментами. В тих перерізах, де моменти менші, частину арматури, з метою її економії, можна обірвати. Арматурні стержні обриваються попарно.
Визначимо
несучу здатність перерізу, армованого стержнями верхнього ряду, на опорі 3, 4Æ28 А-ІІ, ![]() = 24,63 см2.
Робоча висота
= 24,63 см2.
Робоча висота
h01 = hb – tb – d – u/2 = 45 – 3 – 2,8 – 3/2 = 37,7 cм.
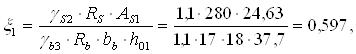 за табл. 7.17
[5] η = 0,701.
за табл. 7.17
[5] η = 0,701.
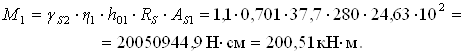
Несуча
здатність перерізу, армованого 2Æ 28 А-ІІ, ![]() .
.
h02 = hb – tb – d/2 = 45 – 3 – 2,8/2 = 40,6 cм.
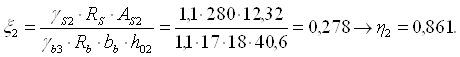
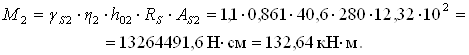
В
прольотах переріз балки армовано 2Æ18 + 2Æ16 А-ІІ,![]() , h01 = 38,7
см; x1 = 0,215; h1 = 0,892; М1 = 96,86
кН·м.
, h01 = 38,7
см; x1 = 0,215; h1 = 0,892; М1 = 96,86
кН·м.
Несуча
здатність перерізу, армованого 2Æ 18 А-ІІ, ![]() = 5,09 см2:
= 5,09 см2:
h02 = 41,1 см; x2 = 0,113; h2 = 0,943; М2 = 60,76 кН·м.
Відкладаючи в масштабі величини знайдених моментів, знаходимо точки теоретичного обриву стержнів і будуємо епюру матеріалів (рис. 3.4). Надійна робота обірваних стержнів буде забезпечена, якщо вони будуть заведені за місце теоретичного обриву на довжину анкеровки
![]()
де 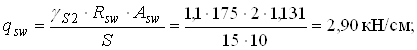
Крок
поперечних стержнів s=150 мм і величина поперечної сили Q1=53 кН в місці
теоретичного обриву стержнів взяті з рис. 3.4. Так як ![]() , то приймаємо
, то приймаємо ![]() . Таким чином знаходимо
величини зон анкеровки і для останніх стержнів.
. Таким чином знаходимо
величини зон анкеровки і для останніх стержнів.
4. Розрахунок рами акведука
4.1 Статичний розрахунок рами
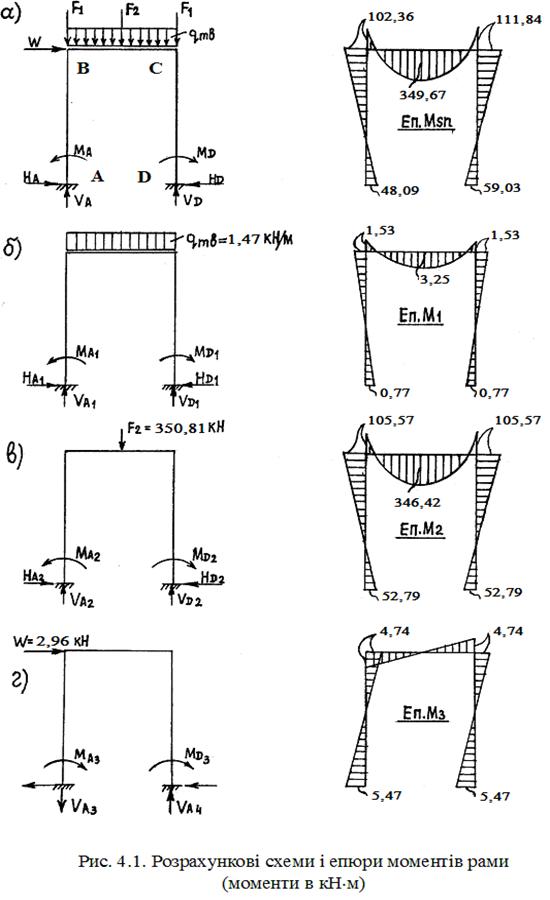
Рама акведука являє собою три рази статично невизначену систему, так як ригель з колонами і колони з фундаментами з’єднані жорстко. Рама навантажена зосередженими силами F1 і F2 у місцях обпирання другорядних балок і рівномірно розподіленим навантаженням по всій довжині ригеля qmb від власної ваги, а також горизонтальною зосередженою силою W від вітру, прикладеною по осі ригеля (рис. 4.1, а).
Величини зосереджених сил :
F1=0,5 · qb · lb + g (ρb · hs · γf b + ρsc · hsc · γfc) · (hw + 0,2) · lb =
= 0,5·58,47 ·6,0+10 ·(2,5 · 0,17 · 1,05 + 1,8 · 0,02 · 1,2) · (1,7 + 0,2)·6,0=231,21 кН;
F2 = qb · lb = 58,47 · 6,0 = 350,82 кН.
Рівномірно розподілене навантаження від власної ваги ригеля
qmb = g ·ρb · bmb ·(hmb – hs) · γf b = 10 · 2,5 · 0,2 · (0,5 – 0,17) · 1,05 = 1,47кН/м.
Зосереджене зусилля від тиску вітру
W =с ·W0 · γf · lb ·(hw + hb)=1,4 · 0,24 · 1,4 · 6,0 · (1,7 + 0,45) = 2,96 кН,
де γf = 1,4 – коефіцієнт надійності за навантаженням для вітру,
с - сумарний аеродинамічний коефіцієнт.
За формулами додатку 9 [2] знаходимо розрахункові зусилля у перерізах рами від дії зовнішніх навантажень.
Коефіцієнт k обчислюємо за формулою
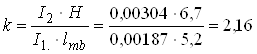 ,
,
де момент інерції стояка
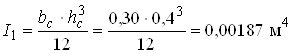 ;
;
момент інерції ригеля в монолітному залізобетоні
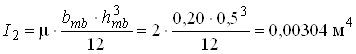 ,
,
приймаємо μ = 2 (для монолітного акведука).
Зусилля за першою схемою завантаження (рис. 4.1, б)
![]() ;
;
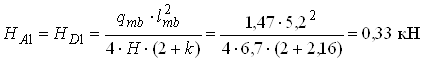 ;
;
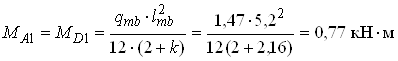 ;
;
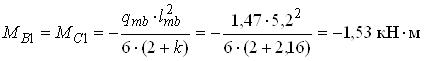 ;
;
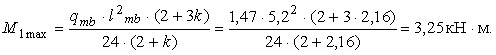
Зусилля за другою схемою завантаження (рис. 4.1, в)
![]() кН;
кН;
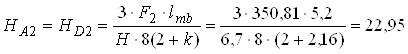 кН;
кН;
![]() кН·м;
кН·м;
![]() кН·м;
кН·м;
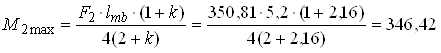 кН·м.
кН·м.
За третьою схемою завантаження (рис. 4.1, г)
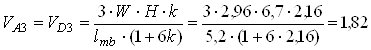 кН;
кН;
![]()
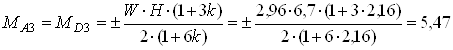 кНм;
кНм;
![]() кН·м;
кН·м;
Складуючи значення зусиль у відповідному перерізі за трьома схемами завантаження і враховуючи сили F1 = 231,21 кН, отримаємо для вихідної розрахункової схеми рами такі зусилля:
VA = 408,62 кН; VD = 412,26 кН; MВ = 102,36 кН·м;
HA = 21,8 кН; HD = 24,76 кН; МС = 111,84 кН·м;
MA = 48,09 кН·м; MD = 59,03 кН·м; Msn = 349,67 кН·м.
4.2 Розрахунок ригеля рами
4.2.1 Розрахунок міцності нормальних перерізів ригеля
Матеріали ригеля такі ж, як і другорядної балки. Мінімальна робоча висота перерізу
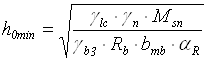 =
=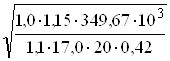 = 50,6см,
= 50,6см,
де ξR = 0,6 – значення граничної відносної висоти стиснутої зони, визначене за табл. додатку 8 [2]. Йому відповідає αR = 0,42.
![]() .
.
Прийняті раніше розміри перерізу балки недостатні. Приймаємо розміри
hmb ´ bmb = 60 ´ 20 см2
Розрахункову висоту перерізу визначаємо з умови розміщення робочої арматури у два ряди по висоті перерізу
ho = hmb – tb – d – u / 2 =60 –3 – 2 – 3/2 = 53,5 см.
Потрібну площу перерізу арматури на опорах за моменту Мс = 111,84 кН·м визначаємо у такій послідовності:
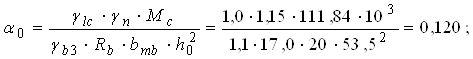
за α0 = 0,120 знаходимо η = 0,935 (табл. 7.17 [5]).
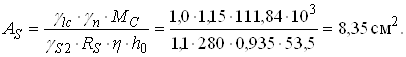
Приймаємо 4 Æ 18 А-ІІ, As = 10,18 см2.
Обчислюємо площу перерізу арматури у прольоті. Msn=207,78 кН·м. Розрахунковий переріз ригеля у прольоті буде залежати від випадку розташування нейтральної лінії. Визначимо ширину полиці ригеля, що вводиться у розрахунок,
![]() = bmb + 2bef =
20 + 2 · 100 = 220 см,
= bmb + 2bef =
20 + 2 · 100 = 220 см,
де ширина звисання bef, яку приймаємо у розрахунках із умов:
bef ![]() 0,5 · lef =
0,5 · 242 = 121,0 см;
0,5 · lef =
0,5 · 242 = 121,0 см;
bef ![]() 1/6 · lb = 1/6
· 600 = 100,0 см.
1/6 · lb = 1/6
· 600 = 100,0 см.
Приймаємо
для розрахунку ![]() = 220 см.
= 220 см.
Визначаємо випадок розташування нейтральної лінії
![]()
![]()
Нейтральна вісь проходить у поличці.
Розрахунковий
переріз ригеля буде прямокутний з розмірами ![]() ´ h0 = 220 ´ 53,5 cм. Тоді
´ h0 = 220 ´ 53,5 cм. Тоді
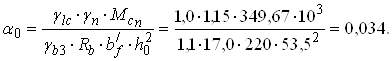
За α0 = 0,034 знаходимо η = 0,983 (табл. 7.7 [5]).
Необхідна площа перерізу арматури
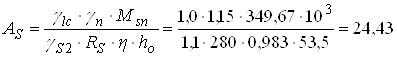 см2.
см2.
Приймаємо 4 Æ 28 А-ІІ, AS = 24,63 см2 (табл. 5.41 [5]).
4.2.2 Розрахунок міцності похилих перерізів ригеля
Розрахункова поперечна сила
Q = VD – F1 = 412,26 – 231,21 = 181,05 кН.
Поперечну
арматуру можна не розраховувати на сприйняття поперечної сили, коли бетон
сприймає дію цієї сили, тобто ![]() . Враховуючи, що найбільш
невигідна похила тріщина йде від опори ригеля до першої зосередженої сили,
проекція найбільш невигідної похилої тріщини
. Враховуючи, що найбільш
невигідна похила тріщина йде від опори ригеля до першої зосередженої сили,
проекція найбільш невигідної похилої тріщини ![]() м. Тоді поперечна сила, яку
сприймає бетон, визначиться за формулою
м. Тоді поперечна сила, яку
сприймає бетон, визначиться за формулою
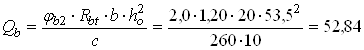 кН,
кН,
але
вона повинна бути не менше ![]() і не більше
і не більше ![]() , які обчислюються за
формулами:
, які обчислюються за
формулами:
![]() кН;
кН;
![]() кН.
кН.
Оскільки
![]() , потрібно
виконати розрахунок поперечних стержнів.
, потрібно
виконати розрахунок поперечних стержнів.
Приймаємо поперечну арматуру Æ 8 класу А-І (додаток 7 [2]).
Погонне зусилля у поперечній арматурі
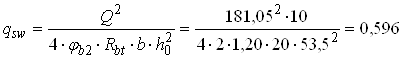 кН/см,
кН/см,
де φb2 = 2 – для важкого бетону.
Довжина проекції похилої тріщини
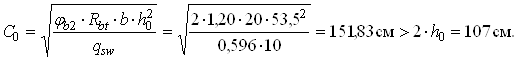
Отримане значення С0 приймається в розрахунок не більше 2·h0.
Приймаємо С0 = 2 · h0 = 107 см.
Погонне зусилля в поперечній арматурі
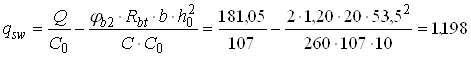 кН/см.
кН/см.
Мінімальне погонне зусилля у поперечній арматурі
![]()
Розрахунковий крок хомутів
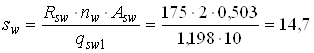 см,
см,
де nw = 2 – кількість поперечних стержнів в одному перерізі ригеля.
Крок поперечних стержнів за конструктивними вимогами
sw,к = h / 3 = 60 / 3 = 20 см.
Приймаємо крок поперечних стержнів sw = 100 мм. З таким кроком поперечна арматура розміщена на приопорних ділянках ригеля (від опори до зосередженої сили). На середній ділянці ригеля крок поперечної арматури
![]() . Приймаємо sw
= 350 мм.
. Приймаємо sw
= 350 мм.
4.2.3 Розрахунок на відрив
В рамі із монолітного залізобетону навантаження від другорядної балки передається на спеціальну поперечну арматуру, яку проектуємо у вигляді сіток.
Площу поперечного перерізу арматури сіток знаходимо за формулою
![]() ,
,
де F2 = 350,81 кН – зусилля, яке знаходимо при статичному розрахунку рами;
Rs – розрахунковий опір сталі класу А-ІІ.
Сітки влаштовуємо на ділянці ригеля
![]() ,
,
де ![]() із розрахунку
міцності нормальних перерізів другорядної балки (опора 1).
із розрахунку
міцності нормальних перерізів другорядної балки (опора 1).
Приймаємо 5 Æ 20 А-ІІ, As = 15,71 см2 з кроком s = 100 мм.
4.3 Розрахунок і конструювання колони
Колона, сприймаючи дію згинаючого моменту і поздовжньої сили, працює на позацентровий стиск. Розрахункова довжина колони у площині рами l0 = 2H. При розрахунку міцності колони її висоту приймають рівною віддалі від обрізу фундаменту до осі ригеля. У нашому випадку
H = Hпідошв. – hf – hmb / 2 = 7,7-0,8 – 0,6 / 2 = 6,6 м = 660 см.
Тоді l0 = 2 · 6,6 = 13,2 м.
Матеріал колони: бетон класу В30 – Rb = 17 МПа; Eb = 3,5·104 МПа (табл. 7.3 і 7.5 [5]); арматура класу А-ІІ – Rs = 280 МПа; Es = 2,1·105 МПа (табл. 7.8 і 7.11 [5]).
Переріз І-І (біля ригеля). Визначаємо розрахункові зусилля. Згинаючі моменти від дії:
а) всіх навантажень
M1 = Mc – HD · 0,5 · hmb = 111,84 – 24,76 · 0,5 · 0,6 = 104,41 кН·м;
б) тривалих навантажень
M1,l = MC,l – HD,l · 0,5 · hmb = 107,1 – 23,28 · 0,5 · 0,6 = 100,12 кН·м,
де HD,l = HD – HD3 = 24,76 – 1,48 = 23,28 кН;
MС,l = MС – MC,3 = 111,84 – 4,74 = 107,1 кН·м.
Нормальні поздовжні сили від дії:
а) всіх навантажень N1 = VD = 412,26 кН;
б) тривалих навантажень N1,l = VD,l = VD –VD3 = 412,26 –1,82= 410,44 кН.
Визначаємо ексцентриситети
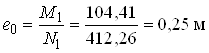 ;
; 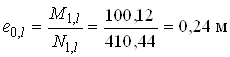 .
.
Робоча висота перерізу h0 = hc – а = 40 – 4 = 36 см.
Гнучкість колони l0 / hc = 13,2/ 0,36 = 37,1 > 10, необхідно врахувати прогин елемента. Вплив прогину враховується коефіцієнтом
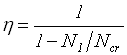 ,
,
де Ncr – умовна критична сила, яку можна обчислити за формулою
 ,
,
де I, Is – моменти інерції відповідно перерізу бетону та арматури:
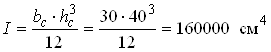 ;
;
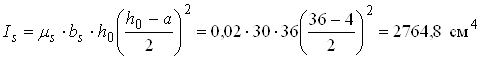 ;
;
де μs
– коефіцієнт армування, попередньо задаємося ![]() .
.
φl – коефіцієнт, який враховує вплив тривалого навантаження
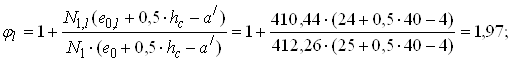
 ;
;
δе – відносний ексцентриситет e0 / hc, який приймають не меншим
δе,min = 0,5 – 0,01 · l0 / hc – 0,01 · Rb = 0,5 – 0,01 · 37,1 – 0,01 · 17 = 0,041.
У нашому випадку
δе = e0 / hc = 25 / 40 = 0,625.
Підставивши значення величин у формулу для обчислення критичної сили, одержимо
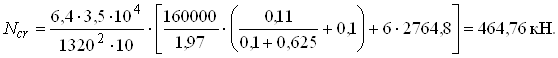
Так як Ncr = 464,76 кН > N1 = 412,26 кН, то переріз колони достатній для сприйняття зусилля
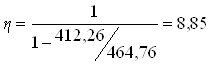 .
.
Визначаємо ексцентриситет сили відносно центра ваги арматури As з врахуванням прогину
e = e0 · η + hc / 2 – a = 25 ·8,85 + 40 / 2 – 4 = 237,25 см.
Попередньо знаходимо відносну висоту стиснутої зони бетону
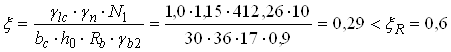 .
.
Площа стиснутої арматури
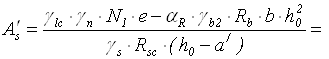
![]() см2
см2
За мінімально допустимим процентом армування площа перерізу
![]()
Приймаємо 2Æ 25А-ІІ, As =9,82 см2 (табл. 5.41 [5]).
Дійсне значення α0
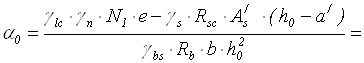
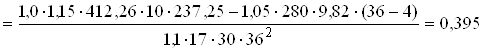 .
.
α0
= 0,395 ![]() ξ
= 0,543 <
ξ
= 0,543 < ![]() .
.
Потрібна площа розтягнутої арматури
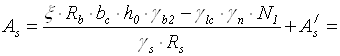
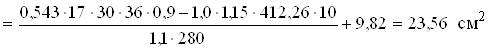 .
.
Приймаємо 4 Æ 28, А-ІІ, As = 24,63 см2.
Фактичний коефіцієнт армування
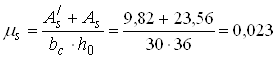
Розбіжність
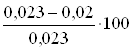 % = 13,04%
< 15%.
% = 13,04%
< 15%.
Розрахунок колони в перерізі ІІ–ІІ (біля фундаменту).
При визначенні поздовжньої сили у перерізі ІІ–ІІ необхідно врахувати власну масу колони
σc = bc · hc ·H · ρb ·γfb = 0,3· 0,4 · 6,60 · 25 · 1,1 = 22,04 кН.
Визначаємо розрахункові зусилля в перерізі ІІ–ІІ.
Згинаючі моменти від дії :
а) всіх навантажень М2 = МD = 59,03 кН·м;
б) тривалих навантажень M2,l = MD – MD4 = 53,56 кН·м.
Нормальні поздовжні сили від дії:
а) всіх навантажень N2 =N1 + σc = 412,26 +22,04 = 434,3 кН;
б) тривалих навантажень N2,l = VD,l + σc = 410,44 + 22,04 = 432,48 кН.
Визначаємо значення ексцентриситетів:
e0 = M2 / N2 = 59,03 / 434,3 = 0,14 м;
e0l = M2l / N2l = 53,56 / 432,48 = 0,12 м.
Відносний ексцентриситет
δe = e0 / hc = 14 / 40 = 0,35;
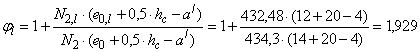 .
.
Задаємося коефіцієнтом армування μ = 0,015.
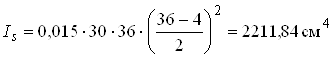 ;
;
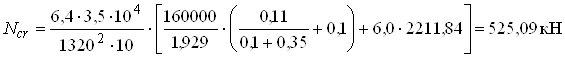
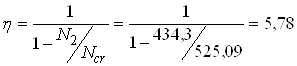
Розрахунковий ексцентриситет
e = e0 · η + hc / 2 – a = 14 · 5,78 + 40 / 2 – 4 = 96,92 см.
Орієнтовна відносна висота стиснутої зони
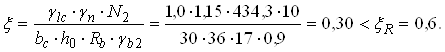
Площа стиснутої арматури
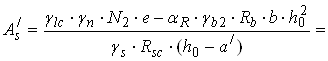
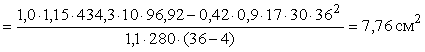 .
.
Мінімально допустима площа перерізу арматури
Asmin = μmin · b · h0 = 0,0025 · 30 · 36 = 2,7 см2.
Приймаємо 2 Æ 25 А-ІІ, As = 9,82 см2.
Дійсне значення a0
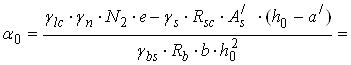
![]() .
.
За ![]() . x=0,371< xК=0,6. Потрібна площа
розтягнутої арматури
. x=0,371< xК=0,6. Потрібна площа
розтягнутої арматури
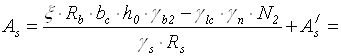
=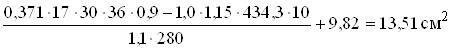 .
.
Приймаємо 3Æ 25 А-ІІ, As = 14,73 см2.
Фактичний коефіцієнт армування
![]()
Розбіжність
![]() % = 11,7%
< 15%.
% = 11,7%
< 15%.
Поперечну
арматуру приймаємо з класу А-І Æ 8. Крок поперечний
арматури ![]() .
Приймаємо s=300 мм.
.
Приймаємо s=300 мм.
Плоскі каркаси об’єднують у просторові за допомогою стержнів(шпильок) діаметром 8 мм з класу А-І. Крок цих стержнів дорівнює кроку поперечної арматури.
5. Розрахунок фундаменту
На рівні верха фундаменту діють зусилля: поздовжня сила N=N2=434,3 кН; згинаючий момент M=MD=59,03 кН·м; поперечна сила Q=HD=24,76 кН. Фундаменти виконані з бетону класу В15 (Rbt = 0,75 МПа) і арматури класу А-ІІІ (Rs = 355 МПа). Розрахунковий опір грунту R0 = 0,19 МПа.
5.1 Визначення розмірів підошви фундаменту
Розміри підошви фундаменту можуть бути визначені за формулами
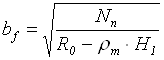 ;
; 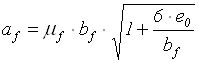 ,
,
де е0 - ексцентриситет сил на рівні підошви фундаменту
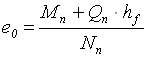 ;
;
Mn, Nn, Qn – згинаючий момент, поздовжня і поперечна сили від нормативних навантажень
![]() кН·м;
кН·м; 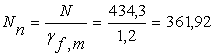 кН;
кН;
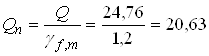 кН;
кН;
γf,m = 1,2 – середній коефіцієнт надійності за навантаженням;
hf – висота фундаменту, прийнята раніше рівною 80 см;
![]()
H1 = 1,5 м – глибина закладання фундаменту;
ρm = 20 кН /м3 середня густина матеріалу фундаменту і грунту на його уступах.
Необхідна ширина підошви фундаменту
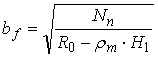
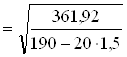 =1,50 м.
=1,50 м.
За відношенням e0 / bf = 0,18 / 1,5 = 0,12 за додатком 10 [2] знаходимо коефіцієнт μ = 0,958.
Довжина підошви фундаменту
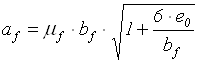
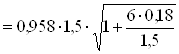 = 1,88 м.
= 1,88 м.
Приймаємо розміри підошви фундаменту af ´ bf = 190 ´ 150 см.
Визначаємо максимальний і мінімальний тиск під підошвою фундаменту від дії нормативних навантажень.
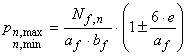 ,
,
де Nf,n – нормальне зусилля на рівні підошви фундаменту від нормативних навантажень з врахуванням ваги фундаменту і грунту на його уступах
Nf,n = Nn + ρm · H1 · af · bf = 361,92 + 20 · 1,5 · 1,9 · 1,5 = 447,42 кН.
Обчислюємо ексцентриситет сили Nf,n на рівні підошви фундаменту
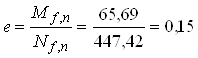 м,
м,
де Mf,n – згинаючий момент від нормативних навантажень на рівні підошви фундаменту
Mf,n = Mn + Qn · hf = 49,19 + 20,63 · 0,8 = 65,69 кН·м.
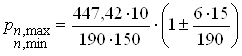 ; рn,max = 0,231
МПа; рn,min = 0,08 МПа.
; рn,max = 0,231
МПа; рn,min = 0,08 МПа.
рn,max = 0,231 МПа > 1,2 · R0 = 1,2 · 0,19 = 0,228 МПа;
рn,min = 0,08 МПа > 0.
У нашому випадку перша умова не виконується. Збільшимо розміри підошви, приймаючи af ´ bf = 200 ´ 150 см, тоді:
Nf,n = 361,92 + 20 · 1,5 · 2,0 · 1,5 = 451,92 кН;
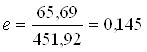 м. ® m1=0,97.
м. ® m1=0,97.
рn,max = 0,216 МПа < 1,2 · R0 = 1,2 · 0,17 = 0,228 МПа;
рn,min = 0,085 МПа > 0.
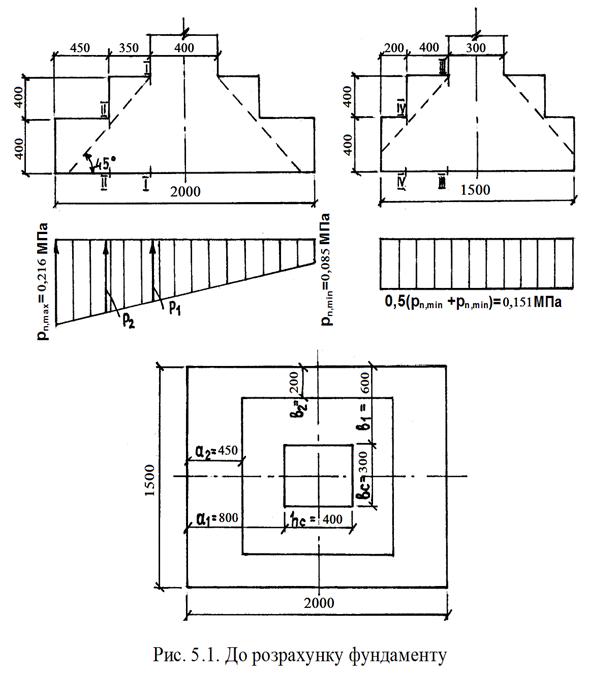
Розміри підошви достатні. Будуємо епюру реактивного тиску грунту на підошву фундаменту (рис. 5.1).
5.2 Визначення необхідної висоти фундаменту
Висоту фундаменту попередньо призначають, виходячи з конструктивних міркувань, а потім перевіряють розрахунком. Із умови анкерування арматури колони
hf > 25 · d= 25 · 28 = 70 см.
Отже, залишаємо попередньо прийняту висоту фундаменту hf =80 см.
Висоту фундаменту перевіряємо із умови продавлювання його по поверхні піраміди (грані піраміди продавлювання показані на рис. 5.1. пунктиром). Продавлююче зусилля від реактивного тиску грунту та опір бетону на зріз по поверхні піраміди продавлювання залежать від співвідношення сторін фундаменту і його висоти. Коли розміри нижньої основи піраміди продавлювання більші розмірів підошви, тобто
ан=hc+2h0>af; bн=hc+2h0>bf,
продавлююча сила відсутня Р=0 і перевірку висоти фундаменту із умови продавлювання не виконують.
Якщо розміри нижньої основи піраміди продавлювання менші розмірів підошви (ан<af; bн<bf), то продавлююча сила визначається за формулою
P=(af bf –aн bн)pmt,
а опір бетону зрізу по поверхні піраміди продавлювання обчислюють за виразом
F = k1 Rbt bm ho,
У тому випадку, коли ан<af, а bн>bf, продавлюючу силу визначають так
P=(af - ан) bf pmax,
а опір бетону зрізу – по формулі
F =0,5 k1 (bс+bf)Rbt ho.
Висота фундаменту буде достатня, коли F³P.
У наведених формулах:
h0 - робоча висота фундаменту, h0=h – a - 0,5d;
hc, - висота і ширина перерізу колони;
k1 - коефіцієнт роботи бетону, для важких бетонів його приймають рівним одиниці;
bm - середній периметр нижньої та верхньої основ піраміди продавлювання
bm= hc+ bс+ ан+ bн;
pmt - середній тиск грунту під підошвою фундаменту від розрахункових зусиль
pmt=0,5(pmax+pmin).
Для нашого випадку
h0=80-7-0,5×1,0=72,5 см;
ан=hc+2h0=40+2×72,5=185 см < af=200 см;
bн=bc+2h0=30+2×72,5=175 см > bf=150см;
Nf=N+rmH1afbf=434,3+20×1,5×2,0×1,5=524,3 кН;
Mf=M+Qhf=59,03+24,76× 0,8=78,84 кН×м;
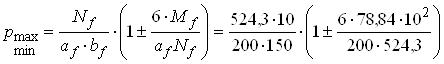 ,
,
pmax=0,254 МПа; pmin=0,0959 МПа.
Продавлююча сила
P=(af - ан) bf pmax=(200-185)150× 0,254×102=57150 Н=57,15 кН.
Опір бетону зрізу
F =0,5k1(bс+bf)Rbtho=0,5×1(30+150)72,5×0,75×102=489375 Н=489,38 кН.
Оскільки F =489,38 кн >P=57,15 кН висота фундаменту достатня.
5.3 Призначення розмірів уступів фундаменту
Розміри уступів призначаємо за умови, що зовнішні поверхні уступів не повинні перетинатись з поверхнею піраміди продавлювання (рис. 5.1).
Фундамент проектуємо з двома уступами висотою нижнього 400 мм і верхнього 400 мм. Висота нижнього уступу повинна бути такою, щоб виконувалась умова
pmax(af - ан) £ 0,9Rbth01,
0,254×102(200-185)=0,381 кН<0,9× 0,75×102(40-7-0,5)=2,194 кН.
Умова виконується. Міцність нижнього уступу забезпечена.
5.4 Розрахунок робочої арматури фундаменту
Фундамент, під дією реактивного тиску грунту, працює на згин. Визначимо згинаючі моменти в небезпечних перерізах у площині, перпендикулярній площині дії зовнішнього моменту. Небезпечні перерізи І–І, ІІ–ІІ (рис. 5.1):
 ;
; 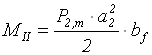 ,
,
де P1,m, P2,m, – середній тиск на підошву по довжині консолей а1, а2 від розрахункових зусиль (рис.5.1).
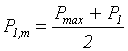 ;
; 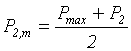 ,
,
P1, P2 – реактивний тиск в перерізах І–І, ІІ–ІІ.
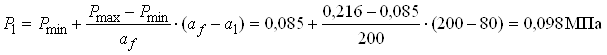
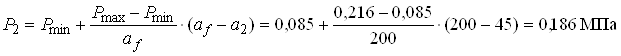
![]() МПа;
МПа; ![]() МПа.
МПа.
Згинаючі моменти
![]() ;
;
![]() .
.
Необхідна площа перерізу робочої арматури
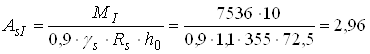 см2;
см2;
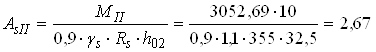 см2.
см2.
Фундаменти армуються сітками з кроком не більше 200 мм, тоді мінімальна кількість стержнів довгого напрямку
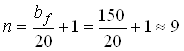 штук.
штук.
Приймаємо 9 Æ 7 А-ІІІ, As = 3,46 см2.
Визначаємо згинаючі моменти у небезпечних перерізах фундаменту в площині, паралельній площині дії зовнішнього моменту. Небезпечні перерізи ІІІ–ІІІ, ІV–IV. (рис.5.1)
 ;
;  ,
,
де ![]() МПа.
МПа.
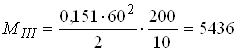 кН·см;
кН·см; 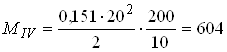 кН·см.
кН·см.
Необхідна площа перерізу арматури
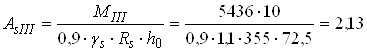 см2;
см2;
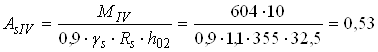 см2
см2
Мінімально допустима кількість стержнів короткого напрямку
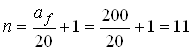 штук.
штук.
Приймаємо 11 Æ 6 А-ІІІ, Asf = 3,113 см2.
Література
1. Бабич Є.М. та ін. Інженерні конструкції – Львів,: вид. Світ, 1991. – 352 с.
2. Бабич Є.М., Погорєляк А.П. Методичні вказівки до виконання курсового проекту з дисципліни “Інженерні конструкції” – Рівне,: 1992. – 55 с.
3. СНиП 2.06.08 – 87. Бетонные и железобетонные конструкции гидротехнических сооружений. – М.: Стройиздат, 1988. – 30 с.
4. СниП 2.03.01-84*. Бетонные и железобетонные конструкции. – М.: Стройиздат, 1989. – 75 с.
5. Бабич В.І., Огороднік В.І., Романюк В.В. Таблиці для проектування будівельних конструкцій. – Рівне; 1999 – 508 с.
6. ВБН В.2.6. – 33 – 2.3 – 01 – 99. Бетонні і залізобетонні конструкції гідротехнічних споруд. – Київ, : 1999. – 106 с.