Главная
Рефераты по зарубежной литературе
Рефераты по логике
Рефераты по маркетингу
Рефераты по международному публичному праву
Рефераты по международному частному праву
Рефераты по международным отношениям
Рефераты по культуре и искусству
Рефераты по менеджменту
Рефераты по металлургии
Рефераты по муниципальному праву
Рефераты по налогообложению
Рефераты по оккультизму и уфологии
Рефераты по педагогике
Рефераты по политологии
Рефераты по праву
Биографии
Рефераты по предпринимательству
Рефераты по психологии
Рефераты по радиоэлектронике
Рефераты по риторике
Рефераты по социологии
Рефераты по статистике
Рефераты по страхованию
Рефераты по строительству
Рефераты по схемотехнике
Рефераты по таможенной системе
Сочинения по литературе и русскому языку
Рефераты по теории государства и права
Рефераты по теории организации
Рефераты по теплотехнике
Рефераты по технологии
Рефераты по товароведению
Рефераты по транспорту
Рефераты по трудовому праву
Рефераты по туризму
Рефераты по уголовному праву и процессу
Рефераты по управлению
Курсовая работа: Определение спектра амплитудно-модулированного колебания
Курсовая работа: Определение спектра амплитудно-модулированного колебания
Пензенский государственный университет
Кафедра «РТ и РЭС»
КУРСОВОЙ ПРОЕКТ
по курсу «Радиотехнические цепи и сигналы»
на тему
«Определение спектра
амплитудно-модулированного колебания»
Задание выполнил студент
группы 01РР2
Чернов С. В.
Задание проверил
Куроедов С. К.
Пенза 2003
Содержание
1. Формулировка задания . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
2. Шифр задания и исходные данные . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
3. Аналитическая запись колебания UW(t) . . . . . . . . . . . . . . . . . . . . . . . . . 3
4. Определение коэффициентов аn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
5. Определение коэффициентов bn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
6. Определение постоянной составляющей А0 . . . . . . . . . . . . . . . . . . . . . 6
7. Определение амплитуд An и начальных фаз Yn . . . . . . . . . . . . . . . . . . 7
8. Временная диаграмма колебания, представляющего собой сумму
найденной постоянной составляющей и первых пяти гармоник
колебания uW(t) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
9. Построение графиков АЧХ и ФЧХ ограниченного спектра
колебания uW(t) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
10. Аналитическая запись АМ колебания . . . . . . . . . . . . . . . . . . . . . . . . . 9
11. Построение графиков АЧХ и ФЧХ АМ колебания . . . . . . . . . . . . . . 11
12. Определение ширины спектра АМ колебания. . . . . . . . . . . . . . . . . . . 12
1. Формулировка задания
Определить спектр АМ колебания u(t) =Um(t)cos(w0t+y0), огибающая амплитуды которого связана линейной зависимостью с сигналом сообщения Uc(t), т.е. Um(t).=U0+ Uc(t)
(коэффициент пропорциональности принят равным единице).
Сигнал сообщения Uc(t) представляет собой сумму первых пяти гармоник
периодического колебания uW(t) (см. раздел 3). Найденный аналитически спектр
сигнала сообщения и АМ колебания должен быть представлен в форме
амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристик. Необходимо
кроме того определить парциальные коэффициенты глубины модуляции mn. Несущая частота определяется как w0=20W5, где W5 –
частота пятой гармоники в спектре колебания uW(t).
Значение амплитуды U0 несущей
частоты w0
принимается равным целой части удвоенной суммы ![]() ,
где Un – амплитудное значение гармоники спектра колебания uW(t).
,
где Un – амплитудное значение гармоники спектра колебания uW(t).
2. Шифр задания и исходные данные
Шифр задания: 17 – 3
Исходные данные приведены в таблице 1.
Таблица 1.
|
U1, В |
U2, В |
T, мкс |
t1, мкс |
| 3 | 3 | 250 | 60 |
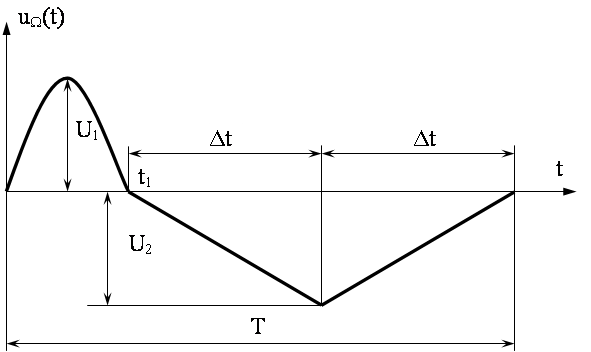
Временная диаграмма исходного колебания
 |
|||
 |
|||
3. Аналитическая запись колебания UW(t)
Сначала выполним спектральный
анализ заданного колебания uΩ(t). Для этого, пользуясь графической формой колебания и
заданными параметрами, запишем его аналитически. Весь период Т колебания
разбиваем на три интервала: [0;t1], [t1;t2] и [t2; T] (точка ![]() является
серединой интервала [t1; T]).
Первый интервал представлен синусоидой, второй и третий – линейными функциями.
В общем виде аналитическая запись сигнала будет выглядеть так:
является
серединой интервала [t1; T]).
Первый интервал представлен синусоидой, второй и третий – линейными функциями.
В общем виде аналитическая запись сигнала будет выглядеть так:
![]()
![]() при
при
![]() ,
,
uΩ(t)= ![]() при
при
![]() ,
(1)
,
(1)
![]() при
при ![]() .
.
Частота синусоиды ![]() (в знаменателе записан
период этой синусоиды).
(в знаменателе записан
период этой синусоиды).
Значения k1 и b1 определяем из системы уравнений
![]() ;
;
![]() ,
,
получаемой путем подстановки во второе уравнение
системы (1) значений времени t1 и ![]() и соответствующих им
значений колебания uΩ(t) (uΩ(t1)=0, uΩ(t)=-U2).
Решение указанной системы уравнений дает
и соответствующих им
значений колебания uΩ(t) (uΩ(t1)=0, uΩ(t)=-U2).
Решение указанной системы уравнений дает ![]() ,
,
![]() . Аналогично определяем k2 и b2. В
третье уравнение системы (1) подставляем значения t2 и T и соответствующие им значения колебания uΩ(t) (uΩ(t2)=-U2, uΩ(T)=0).
. Аналогично определяем k2 и b2. В
третье уравнение системы (1) подставляем значения t2 и T и соответствующие им значения колебания uΩ(t) (uΩ(t2)=-U2, uΩ(T)=0).
![]() ;
;
![]() .
.
Решив систему, получаем ![]() ,
, ![]()
В результате изложенного система уравнений (1) принимает вид
![]()
![]() при
при ![]() ,
,
uΩ(t)= ![]() при
при ![]() , (2)
, (2)
![]() при
при ![]() .
.
Для дальнейших расчетов определим:
![]() мкс;
мкс;
![]() рад/с
рад/с
![]()
![]()
![]()
![]()
![]() рад/с
рад/с
Для разложения сигнала в ряд Фурье вычислим значения аn, bn, Аn и φn первых пяти гармоник.
4. Определение коэффициентов an
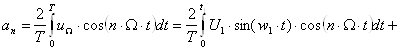

Посчитаем каждый из интегралов отдельно:
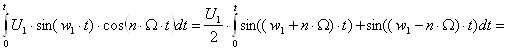
![]()
![]()
![]() ;
;
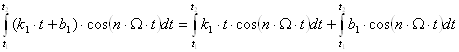 ,
,
первый интеграл интегрируем по частям:
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
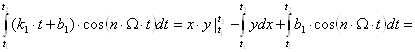
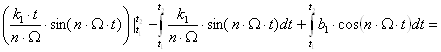
![]()
![]() ;
;
аналогично интегрируем:
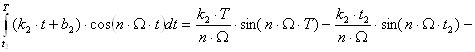
![]() .
.
Запишем выражение для аn, как функции порядкового номера n гармоник колебания UW(t):
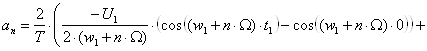
![]()
![]()
![]()
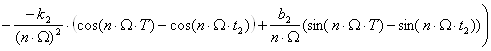 .
.
Подставляя ранее вычисленные значения k1 b1, k2, b2, заданное значение U1 и значения n=1,2,…, находим численные значения пяти коэффициентов an:
![]() В
В
![]() В
В
![]() В
В
![]() В
В
![]() В.
В.
Заносим полученные результаты в таблицу 2.
5. Определение коэффициентов bn
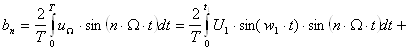
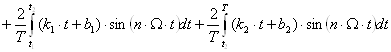 .
.
Расчет каждого из интегралов произведём отдельно:
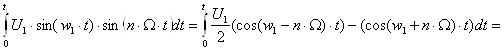
![]() ;
;
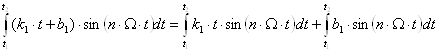
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
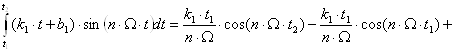
![]() ;
;
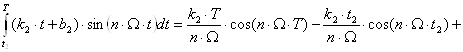
![]() .
.
Запишем выражение для bn, как функции порядкового номера n гармоник колебания UW(t):
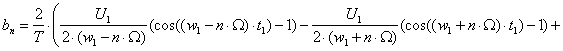
![]()
![]() .
.
Подставляя ранее вычисленные значения k1 b1, k2, b2, заданное значение U1 и значения n=1,2,…, находим численные значения пяти коэффициентов bn:
![]() В
В
![]() В
В
![]() В
В
![]() В
В
![]() В.
В.
Занесём полученные данные в таблицу 2.
6. Определение постоянной составляющей А0
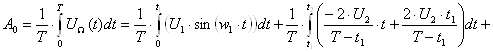
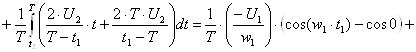
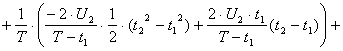
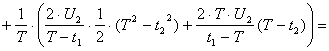
![]()
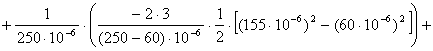
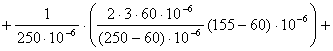
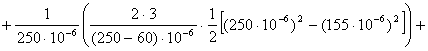
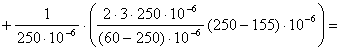
![]() В.
В.
7. Определение амплитуд An и начальных фаз Yn
Значения An и Ψn вычисляем с помощью полученных ранее коэффициентов an и bn.
![]() ,
,
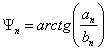 .
.
![]() В,
В,
![]() В,
В,
![]() В,
В,
![]() В,
В,
![]() В;
В;
![]() рад,
рад,
![]() рад,
рад,
![]() рад,
рад,
![]() рад,
рад,
![]() рад.
рад.
Полученные результаты заносим в таблицу 2.
Таблица 2
| n | 1 | 2 | 3 | 4 | 5 |
|
an |
1.641 | 0.033 | -0.368 | -0.237 | -0.128 |
|
bn |
1.546 | 0.548 | 0.442 | 0.028 | -0.093 |
|
An |
2.254 | 0.549 | 0.575 | 0.239 | 0.159 |
|
Ψn |
0.756 | 1.511 | 2.264 | 3.023 | -2.512 |
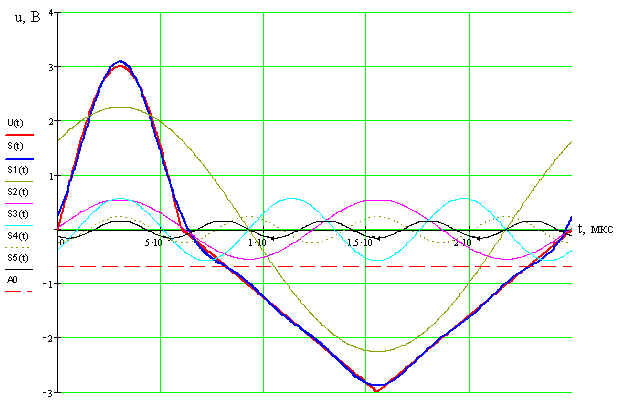
8. Временная диаграмма колебания, представляющего собой сумму найденной постоянной составляющей и первых пяти гармоник
|
|
|
|
|
|
|
|
|
|
|
u(t) – заданное колебание,
S(t)=S1(t)+ S2(t)+ S3(t)+ S4(t)+ S5(t)+A0,
S1(t) – первая гармоника,
S2(t) – вторая гармоника,
S3(t) – третья гармоника,
S4(t) – четвертая гармоника,
S5(t) – пятая гармоника,
A0 – постоянная составляющая.
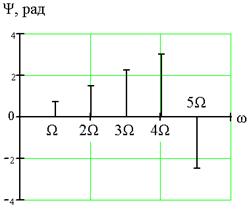
9. Построение графиков АЧХ и ФЧХ ограниченного спектра колебания uW(t)
Пользуясь данными таблицы 2, строим АЧХ и ФЧХ сигнала сообщения uc(t), представляющего собой, в соответствии с заданием, сумму первых пяти гармоник колебания uW(t).
АЧХ колебания uW(t)
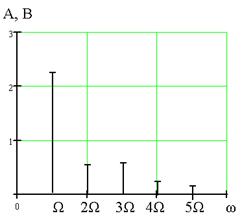
ФЧХ колебания uW(t)
|
|
10. Аналитическая запись АМ колебания
В качестве модулирующего колебания (сигнала сообщения) используем только первые пять гармоник спектра колебания uW(t) (постоянную составляющую А0 отбрасываем). В соответствии с этим искомое амплитудно-модулированное колебание запишем как
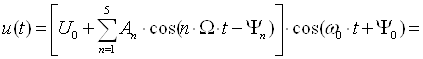
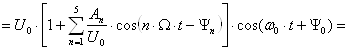
![]()
![]() рад/с – несущая частота.
рад/с – несущая частота.
Значение амплитуды U0 несущей частоты w0
принимается равным целой части удвоенной суммы ![]() ,
где Un – амплитудное значение гармоники спектра колебания UW(t).
,
где Un – амплитудное значение гармоники спектра колебания UW(t).
![]() ,
,
![]() В.
В.
![]() – начальная фаза несущего колебания.
– начальная фаза несущего колебания.
![]() – парциальные коэффициенты глубины модуляции.
– парциальные коэффициенты глубины модуляции.
Вычислим значения парциальных коэффициентов:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Полученные результаты заносим в таблицу 3.
Представим АМ колебание в форме суммы элементарных гармоник
![]()
![]()
![]() .
.
Вычислим
значения ![]() :
:
![]() В,
В,
![]() В,
В,
![]() В,
В,
![]() В,
В,
![]() В.
В.
Полученные результаты заносим в таблицу 3.
Таблица 3.
| n | 1 | 2 | 3 | 4 | 5 |
|
mn |
0.3221 | 0.0784 | 0.0822 | 0.0341 | 0.0227 |
|
Bn, В |
1.127 | 0.274 | 0.288 | 0.119 | 0.079 |
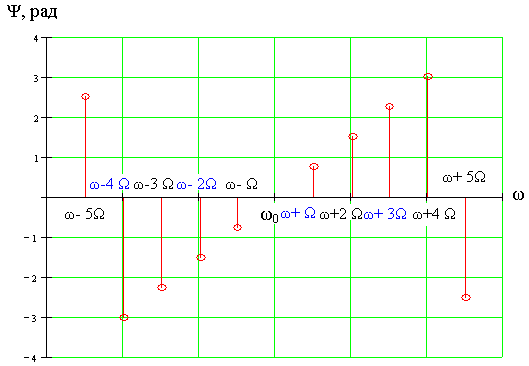
11. Построение графиков АЧХ и ФЧХ АМ колебания
Воспользовавшись численными значениями U0, ω0, Bn, Ω, Ψ0, Ψn, построим графики АЧХ и ФЧХ амплитудно-модулированного колебания.
АЧХ АМ колебания
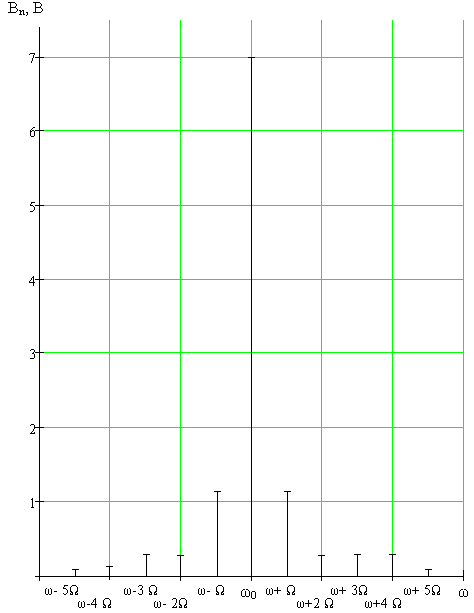
ФЧХ АМ колебания
12. Определение ширины спектра АМ колебания
Ширина спектра АМ колебания равна удвоенному значению наивысшей частоты в спектре модулирующего низкочастотного сигнала.
![]() рад/с.
рад/с.