Лабораторная работа: Корреляционно-регрессионный анализ

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

НОВГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Имени ЯРОСЛАВА МУДРОГО

ИНСТИТУТ ЭКОНОМИКИ И УПРАВЛЕНИЯ

Кафедра: Статистики и экономико-математических методов

Отчет

По дисциплине статистика

Лабораторная работа по теме:

«Корреляционно регрессионный анализ»

Вариант 2

Выполнила студентка гр.8431

Гарбузова Ю.

Егарева Т. Н

Ерошенко Н.Н

Проверила

Фетисова Г.В

Великий Новгород

2010

Корреляционный анализ изучает стохастические связи между случайными величинами в экономике. Метод корреляции применяется для того, чтобы при сложном взаимодействии посторонних влияний выявить зависимость между результатом и факторами в том случае, если посторонние факторы не изменялись и не искажали основную зависимость. При этом число наблюдений должно быть достаточно велико, так как малое число наблюдений не позволяет обнаружить закономерность связи. Укрупненно можно рекомендовать: число наблюдений равно восьмикратному числу факторов, включенных в модель.

Задание:

1.) Построить корреляционное поле зависимости между y и x1. Сделать вывод относительно формы и направления связи.

2.) Построить уравнение регрессии между у и х1 (линейная, степенная, логарифмическая). Оценить каждую функцию через F-критерий, , ошибку аппроксимации.

3.) Построить корреляционное поле зависимости между y и x2. Сделать вывод относительно формы и направления связи.

4.) Построить двухфакторное уравнение регрессии между y, x1,x2. Оценить показатели тесноты связи.

5.) Оценить модель через F-критерий Фишера.

6.) Оценить параметры через t-критерий Стьюдента.

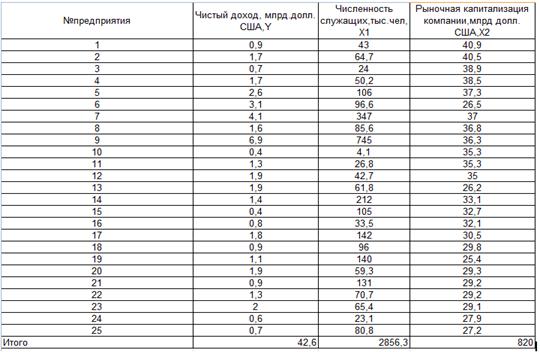
Исходные данные :

Уравнение регрессии между у и х1 (линейная):

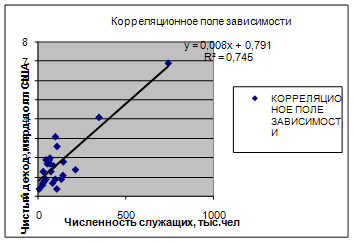
F расч = (0,7451/(1-0,7451))*((25-1-1)/1) = 67,232

Уравнение регрессии между у и х1 (логарифмическая):

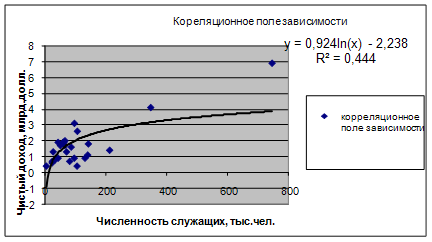
F расч = (0,4445/(1-0,4445))*((25-1-1)/1) = 18,404

Уравнение регрессии между у и х1 (степенная):

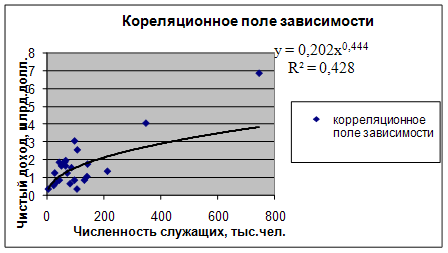
F расч = (0,4284/(1-0,4284))*((25-1-1)/1) = 0,019

линейная	F расч	67,23146332
логарифмическая	F расч	18,40414041
степенная	F расч	0,019459742

Е1	53,9
Е2	72,5
Е3	48,2

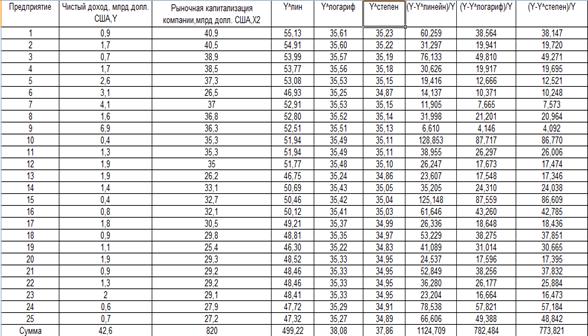
Уравнение регрессии между у и х2 (линейная):

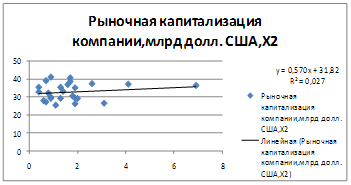
Уравнение регрессии между у и х2(логарифмическая):

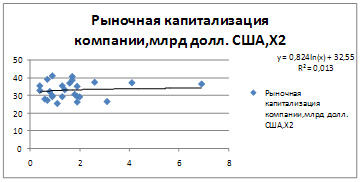
Уравнение регрессии между у и х2(степенная):

E1	2171
E2	166
E3	165

С помощью пакета анализа

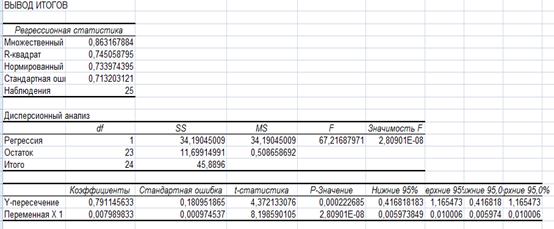
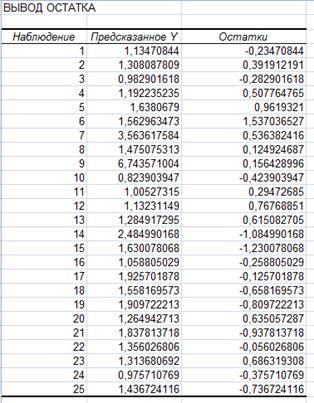
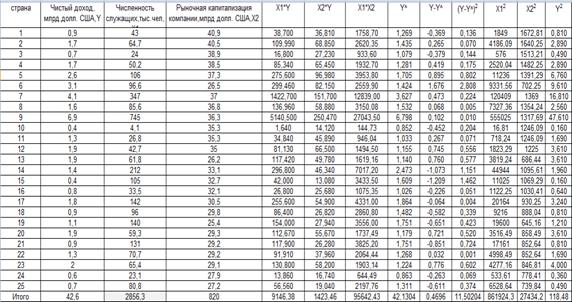
Y=0,148+0,008*x1+0,019*x2

r yx1	0,863
ryx2	0,005
rx1x2	0,395
r yx1x2	0,937
ryx2x1	-0,723
rx1x2y	0,772
R yx1x2	0,937
R^2 yx1x2	0,878
сигма ост	0,003
Fрасч	72,08
Fтабл	2,086
стьюдента	34,40

Линейный коэффициент корреляции может быть определен по формуле:

Или

Он изменяется в диапазоне от -1 до +1. положительный коэффициент характеризует прямую связь, отрицательный – обратную. Связь между факторным и результативным признаком можно признать тесной, если r>0,7.

Индекс корреляции может рассчитываться по формуле:

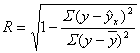Индекс корреляции изменяется от 0 до 1.

оценка существенности связи на основе t – критерия Стьюдента (при оценке параметров) или F – критерия Фишера (при оценке уравнения регрессии).

для линейной формы связи,

для криволинейной формы связи,

где k – число параметров.

Нахождение аппроксимирующего уравнения, для чего определяется средняя ошибка аппроксимации

F-критерия Фишера: