Контрольная работа: Методи перетворення комплексного креслення

Контрольная работа: Методи перетворення комплексного креслення

МЕТОДИ ПЕРЕТВОРЕННЯ КОМПЛЕКСНОГО

КРЕСЛЕННЯ.

ЗМІСТ

Вступ.. 2

1.Заміна площин проекцій.. 3

2. Плоскопаралельне переміщення.. 5

3.Обертання навколо ліній рівня.. 7

4. Косокутне допоміжне проектування.. 10

Висновки.. 11

Список літератури.. 12

Вступ

Розділ геометрії, в якому просторові фігури ( оригінали вивчають за допомогою зображень їхніх графічних моделей на площині малюнка називають нарисною геометрією.

Малюнок повинен нести геометричну інформацію про форму та розміри оригіналу, бути наочним, простим і точним. Формоутворюючими елементами простору є основні геометричні фігури – точка, пряма та площина, з яких утворюються складніші фігури. Геометричною фігурою називають будь – яку непусту множину точок, а геометричний простір може складатися з множини точок, прямих чи площин. Основою нарисної геометрії є метод проекцій, який дає можливість одержувати відображення просторових фігур на площині чи поверхні. За цим методом кожній точці тривимірного простору відповідає певна точка двовимірного простору ( площини ). На площині зображують усі фігури, розміщені в просторі. Перетин проектуючого променя з площиною проекцій дає проекцію точки. Проекцією прямої в загальному випадку є пряма, що проходить через точку її перетину з площиною проекцій. Малюнок, що складається з кількох (мінімум двох) зв'язаних між собою проекцій зображуваної фігури називають комплексним малюнком.

На Мал. 1,а в системі площин проекцій  і  зображено точку А. Перпендикулярно до площини  проводять нову вертикальну площину , на яку ортогонально проектують точку А. Таким чином, замість системи площин проекцій / з проекціями точки  одержують систему / з проекціями точки . При такій заміні відстань від старої проекції до старої осі дорівнює відстані від нової проекції до нової осі. На комплексному рисунку (Мал. 1, б) ці відстані позначено двома рисками. [1] [2]

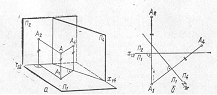
Мал. 1

На Мал. 2 зображено відрізок прямої загального положення АВ. Щоб одержати його натуральну величину, досить провести нову площину паралельно одній з проекцій ( на рисунку вісь  паралельна горизонтальній проекції прямої). Відклавши від нової осі відповідні відстані від фронтальних проекцій точок до старої осі, одержують натуральну величину відрізка .[1]

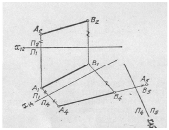
Мал. 2

Для розв’язання ряду метричних задач пряму необхідно поставити в проектуюче положення. Для цього треба скористатися натуральною величиною відрізка. Якщо провести площину, перпендикулярну до неї ( її слід – вісь ), то відклавши відстань, позначену двома рисками, одержимо проекцію прямої у вигляді точки .

На Мал. 3 показано визначення відстані між відрізками двох мимобіжних прямих -  і . Для цього подвійною заміною площин проекцій пряму  проектують в точку, а пряма  спроектувалась при цьому у відрізок . Перпендикуляр, опущений з  на  дає шукану відстань.

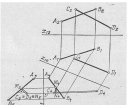
Мал. 3

Крім визначення відстані можна тут же визначити дві найближчі точки  і  на мимобіжних прямих. Показано визначення точок  і . А далі в зворотному напрямі можна визначити точки  і  на полях  та

На Мал. 4 показано визначення натуральної величини трикутного відсіку подвійною заміною площин проекцій. Для цього в площині трикутника спочатку проведено горизонталь . Перпендикулярно до горизонтальної проекції горизонталі вибирають вертикальну площину ( її горизонтальний слід - ), При цьому горизонталь спроектувалася в точку , а весь відсік – у пряму . Паралельно прямій  проводять слід площини  і визначають натуральну величину трикутного відсіку.[1], [2]

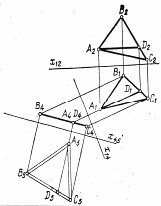
Мал. 4

2. Плоскопаралельне переміщення

Якщо при способі заміни площин проекцій геометричні фігури залишаються на місці, а до них певним чином підбирають площини проекцій, то при способі плоскопаралельного переміщення роблять навпаки: площини проекцій  і  залишають незмінними, а геометричні фігури переміщують певним чином. [1], [3]

На Мал. 5а зображено відрізок прямої загального положення . Для визначення натуральної величини відрізка через його кінцеву точку  проводять вертикальну вісь  , навколо якої відрізок  повертають до фронтального положення. Точка  при цьому переміщується по дузі кола, площина якого перпендикулярна до вертикальної осі , а отже, і горизонтальна. Натуральну величину показано подвійною прямою ()

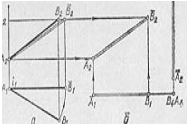
Мал. 5

Цю ж натуральну величину можна одержати без використання зафіксованої осі обертання, досить розмістити пряму паралельно одній з площин проекцій. Тобто цей спосіб, що називають плоскопаралельним переміщенням, є обертанням навколо уявних осей, перпендикулярних до  і .

На Мал. 5б відрізок  розміщено паралельно площині . При цьому кінцеві точки відрізка переміщуються в горизонтальних площинах. Щоб поставити пряму в проектуюче положення, треба в даному випадку натуральну величину відрізка розмістити вертикально; при цьому він переміщується у фронтальній площині.

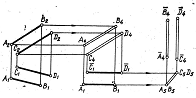
Мал. 6

На Мал.6 показано визначення натуральної величини відстані між двома паралельними прямими загального положення. Спочатку обидва відрізки без зміни їх взаємного положення розміщують паралельно площині , при цьому відрізки зобразяться в натуральну величину. Повернувши відрізки ще раз навколо уявної фронтально проектуючої осі до вертикального положення, одержимо на полі  дійсну величину відстані між паралельними прямими [1].

Визначення натуральної величини двогранного кута показано на

Мал. 7. Для цього ребро двогранного кута , що займає загальне положення, треба поставити в проектуюче положення.

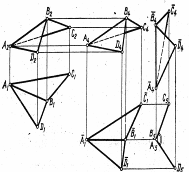
Мал. 7

Спочатку двогранний кут навколо уявної вертикальної осі повертають так, щоб ребро його розмістилося фронтально, другим поворотом навколо уявної фронтально проектуючої осі ребро ставлять у вертикальне положення, при цьому на полі  двогранний кут зобразиться в натуральну величину.

3.Обертання навколо ліній рівня

Крім обертання навколо осей, перпендикулярних до площин проекцій, для розв’язання ряду метричних задач користуються обертанням навколо ліній рівня площин. [3].

На Мал. 8 зображено площину загального положення, задану слідами. Для визначення величини плоского кута, що утворюється в просторі між слідами площини, виконано суміщення відсіку площини служить горизонтальний слід площини .

Мал. 8

Для знаходження суміщеного фронтального сліду на нього вибирають довільну точку , яка при обертанні навколо горизонтального сліду  рухатиметься у вертикальній площині, перпендикулярній до . При цьому відстань від точки збігу слідів площини збережеться, що дозволяє з точки збігу слідів провести дугу кола до перетину в точці  з площиною траєкторії горизонтальної проекції точки. Суміщений фронтальний слід  пройде через точку збігу слідів і знайдено точку [1].

Мал. 9

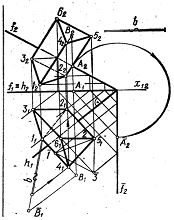
На Мал. 9 зображено площину загального положення, задану слідами, на яку поставлено правильну пряму тригранну призму заввишки . Щоб її поставити, спочатку площину суміщають обертанням навколо горизонтального сліду з полем ; при цьому одержують суміщений фронтальний слід . На суміщеному полі довільно розміщено рівносторонній трикутник , який приймають за нижню основу призми. Через вершини трикутника проводять горизонталі, які зворотним шляхом знаходять на горизонтальній та фронтальній проекціях. Кожна вершина знаходиться на відповідній горизонталі.

Оскільки призма пряма, її бічні ребра будуть перпендикулярними до площини. Тому через усі три вершини нижньої основи призми проводять перпендикуляри до площини : фронтальні проекції ребер перпендикулярно до фронтального сліду, а горизонтальні – перпендикулярно до горизонтального сліду. Для визначення призми заданої висоти на одному з ребер, наприклад на ребрі, що проходить через точку , беруть довільну точку  і визначають способом прямокутного трикутника дійсну величину ребра  ( гіпотенузу ), На цій гіпотенузі від точки  відкладають задану висоту призми , за допомогою якої знаходять горизонтальну проекцію ребра , за ним ребра горизонтальної проекції, а за вертикальною відповідністю – ребра фронтальної проекції [1], [3].

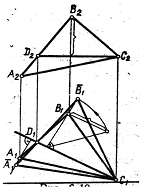
На Мал. 10 способом обертання навколо горизонтальної знайдено натуральну величину трикутного відсіку . Для цього в площині відсіку проведено горизонталь . Трикутний відсік обертають навколо горизонталі до положення, паралельного ; при цьому вершини відсіку  і  обертатимуться у вертикальних площинах, перпендикулярних до . Способом прямокутного трикутника знаходять дійсну величину радіуса обертання для точки . Оскільки точка  залишається на місці, точку  знаходять на перетині обертання точки  навколо горизонталі та прямої .

Мал. 10

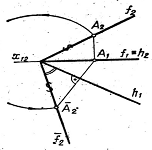
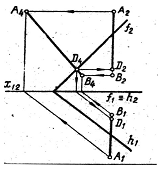
Цей засіб доцільно використовувати для розв'язання позиційних задач. Ідея засобу полягає в тому, що напрям проектування вибирають таким чином, щоб пряма або площина, що розглядається в задачі, зайняла проектуюче положення [1]. На Мал. 11 засіб косокутного допоміжного проектування використано для визначення точки перетину профільної прямої  з площиною загального положення, заданою слідами. Площину та пряму спроектовують на поле  у напрямі горизонтальної площини; при цьому площина спроектувалася своїм фронтальним слідом, а пряма – відрізком . Перетин цих двох прямих – точка , яку у зворотному напрямі проектування знаходять на профільній прямій ().

Мал. 11

Для розв'язання більшості метричних та деяких позиційних задач геометричні фігури загального положення треба привести в окреме положення. Це перш за все стосується прямих ліній, площин, гранних і криволінійних поверхонь. Після перетворення комплексного рисунка додаткові проекції дають можливість розв'язувати задачі простіше.

Методи перетворення проекцій спираються на два основних принципи:

1) зміна взаємного положення об'єкта проектування та площин проекцій

2) зміна напряму проектування.

Перетворення комплексного креслення необхідне для визначення натуральних величин відрізків, відстаней між відрізками, а також відстаней між крапками і площинами. Застосовуючи спосіб зміни площин проекції можна визначити величину кутів між прямими. Поворотом навколо прямій можна ввести крапку в площину, знайти положення крапки, лежачої усередині геометричного тіла.

Засіб косокутного допоміжного проектування використовують для розв'язання позиційних задач.

1. Михайленко В. Є. та ін- Нарисна геометрія - К. Вища школа, 1992. ( гл. 6 )

2. Русскевич Н. Л. Начертательная геометрия –М. Наука, 1976 ( гл.І У)

3. Четверухин Н. Ф. Начертательная геометрия – М. Наука, 1972 ( гл. У)