Главная
Рефераты по зарубежной литературе
Рефераты по логике
Рефераты по маркетингу
Рефераты по международному публичному праву
Рефераты по международному частному праву
Рефераты по международным отношениям
Рефераты по культуре и искусству
Рефераты по менеджменту
Рефераты по металлургии
Рефераты по муниципальному праву
Рефераты по налогообложению
Рефераты по оккультизму и уфологии
Рефераты по педагогике
Рефераты по политологии
Рефераты по праву
Биографии
Рефераты по предпринимательству
Рефераты по психологии
Рефераты по радиоэлектронике
Рефераты по риторике
Рефераты по социологии
Рефераты по статистике
Рефераты по страхованию
Рефераты по строительству
Рефераты по схемотехнике
Рефераты по таможенной системе
Сочинения по литературе и русскому языку
Рефераты по теории государства и права
Рефераты по теории организации
Рефераты по теплотехнике
Рефераты по технологии
Рефераты по товароведению
Рефераты по транспорту
Рефераты по трудовому праву
Рефераты по туризму
Рефераты по уголовному праву и процессу
Рефераты по управлению
Реферат: Лінійна модель виробництва
Реферат: Лінійна модель виробництва
ЛІНІЙНА МОДЕЛЬ ВИРОБНИЦТВА
1. Лінійні моделі виробництва та лінійне програмування
Будь-яке національне господарство розвивається в складній мережі міжгалузевих взаємозв'язків, які зрозуміти шляхом простого математичного апарату неможливо. Наприклад, попит на автомобілі впливає не тільки на автомобільну промисловість, але непрямо і на металургію – виробника базової сировини для виготовлення автомобілів, і на галузі, пов'язані з виробництвом шин, і інших комплектуючих частин, а також на галузі, які виготовляють радіоелектронне устаткування та ін. Прості розрахунки показують, що «лобовий» підхід та арифметика не допоможуть при спробі кількісного аналізу прямого й непрямого ефекту поширення таких впливів.
Метод міжгалузевого аналізу, розроблений американським економістом російського походження Василем Леонтьєвим, дозволяє дати послідовні та чисельно впевнені відповіді на запитання, пов'язані з міжгалузевими взаємодіями й їх впливами на основні макроекономічні показники.
Розглянемо діяльність найнижчої ланки макроекономіки (виробничої одиниці – заводу, цеху). Потрібно скласти план виробництва, який забезпечує максимальний ступень виконання завдання. Щодо даної виробничої одиниці відомі її технічні можливості, а також кількість сировинних ресурсів, які можна використати.
Нехай кількість
всіх видів ресурсів ![]() позначимо їх
позначимо їх ![]() . Це можуть бути метал,
електроенергія, різні види поставок з інших підприємств. Припустимо, що на
виробництві можуть випускатися
. Це можуть бути метал,
електроенергія, різні види поставок з інших підприємств. Припустимо, що на
виробництві можуть випускатися ![]() типів
товарів
типів
товарів ![]() .
.
Технологією
виробництва товарів
![]() назвемо набір чисел
назвемо набір чисел ![]()
![]() , що показують, яка
кількість ресурсів
, що показують, яка
кількість ресурсів ![]() необхідні для
випуску однієї одиниці товару
необхідні для
випуску однієї одиниці товару ![]() . Так
виробництво товарів
. Так
виробництво товарів ![]() можна подати як
конвеєр, протягом якого подаються ресурси в кількості
можна подати як
конвеєр, протягом якого подаються ресурси в кількості ![]() а в кінці конвеєра виходить
готова одиниця продукту
а в кінці конвеєра виходить
готова одиниця продукту ![]() .
.
Отже, можна
скласти технологічну матрицю, яка повністю описує технологічні можливості
виробництва. Позначаємо її через ![]()
 .
.
Нехай задані
кількості ![]() ресурсів
ресурсів ![]() ,
,![]() , які можуть бути
використані у виробництві, тоді
, які можуть бути
використані у виробництві, тоді ![]() –
вектор ресурсів. Назвемо планом виробництва вектор
–
вектор ресурсів. Назвемо планом виробництва вектор ![]() ,
що показує, яка кількість товарів
,
що показує, яка кількість товарів ![]() буде
вироблена.
буде
вироблена.
Вважатимемо
технологію виробництва лінійною, тобто припустимо, що всі витрати ресурсів
зростають прямо пропорційно обсягу випуску. Припустимо, що витрати під час
випуску ![]() одиниць продукту
одиниць продукту ![]() описуються вектором
описуються вектором ![]() , причому одночасне
функціонування декількох технологічних процесів приводить до сумарних витрат.
, причому одночасне
функціонування декількох технологічних процесів приводить до сумарних витрат.
Отже, витрати
ресурсів, необхідні для виконання плану виробництва ![]() ,
описуються вектором, координати якого мають такий вигляд:
,
описуються вектором, координати якого мають такий вигляд:
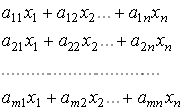
або в матричній
формі вектором ![]() . Умова
обмеженості ресурсів записується у вигляді
. Умова
обмеженості ресурсів записується у вигляді ![]() .
Отже, при заданому векторі ресурсів розглянутою виробничою одиницею може бути
будь-який випущений набір товарів
.
Отже, при заданому векторі ресурсів розглянутою виробничою одиницею може бути
будь-який випущений набір товарів ![]() , який
задовольняє обмеженням
, який
задовольняє обмеженням ![]() ,
, ![]() . Як правило, такий вектор
не єдиний. У зв'язку з цим з'являється можливість вибору найкращого в деякому
розумінні плану.
. Як правило, такий вектор
не єдиний. У зв'язку з цим з'являється можливість вибору найкращого в деякому
розумінні плану.
Розглянемо
можливі постановки оптимізаційної задачі. Нехай задані ціни ![]() на продукти виробництва
на продукти виробництва ![]() . Потрібно визначити план
виробництва, що максимізує вартість продукції. Формальний запис цієї задачі
такий:
. Потрібно визначити план
виробництва, що максимізує вартість продукції. Формальний запис цієї задачі
такий:
![]() ,
, ![]() ,
, ![]() .(1)
.(1)
Така постановка
задачі відповідає принципу планування за валом. Випадок, коли планування
випуску проводиться за номенклатурою товарів, можна змоделювати інакше. Нехай
заданий вектор ![]() , що визначає
один комплект випуску. Потрібно випустити як можна більше таких комплектів.
Нехай
, що визначає
один комплект випуску. Потрібно випустити як можна більше таких комплектів.
Нехай ![]() означає кількість
комплектів, що випускають. Розглянемо задачу
означає кількість
комплектів, що випускають. Розглянемо задачу
![]() ,
, ![]() ,
, ![]() ,
, ![]() .(2)
.(2)
Тут нерівність ![]() означає, що вектор
означає, що вектор ![]() містить не менше
містить не менше ![]() повних комплектів
повних комплектів ![]() продукції, що
випускається.
продукції, що
випускається.
Моделі (1), (2),
хоча й відбивають певні риси реального виробництва, є, значно ідеалізованими.
Так, відсутнє таке важливе для виробництва поняття, як час. Вважається, що всі
необхідні ресурси ![]() ,
, ![]() доступні. Отже, такі
моделі абстраговані від динаміки виробництва й не враховують цілий ряд інших
показників, які є неодмінним атрибутом реального виробництва.
доступні. Отже, такі
моделі абстраговані від динаміки виробництва й не враховують цілий ряд інших
показників, які є неодмінним атрибутом реального виробництва.
Незважаючи на розходження змістовних результатів ілюстративні лінійні моделі (1), (2) мають багато спільного, а саме є стандартними задачами лінійного програмування. Основними обчислювальними схемами розв’язування задач лінійного програмування є симплекс-метод і його модифікації.
2. Статична схема міжгалузевого балансу. Модель Леонтьєва
Основою багатьох
лінійних методів виробництва є схема міжгалузевого балансу. Нехай весь
виробничий сектор народного господарства розбитий на ![]() чистих галузей, тобто
продукція кожної з цих галузей передбачається однорідною. Кожна галузь випускає
продукт тільки одного типу, і різні галузі випускають різні продукти. В процесі
виробництва свого виду продукту кожна галузь потребує продукцію інших галузей.
Чиста галузь є економічною абстракцією , що не обов'язково існує реально.
Подібна ідеалізація виправдана тим, що вона дозволяє провести аналіз
технологічної структури виробництва та розподілу.
чистих галузей, тобто
продукція кожної з цих галузей передбачається однорідною. Кожна галузь випускає
продукт тільки одного типу, і різні галузі випускають різні продукти. В процесі
виробництва свого виду продукту кожна галузь потребує продукцію інших галузей.
Чиста галузь є економічною абстракцією , що не обов'язково існує реально.
Подібна ідеалізація виправдана тим, що вона дозволяє провести аналіз
технологічної структури виробництва та розподілу.
Припустимо тепер,
що в деякий момент часу, наприклад, у році ![]() ,
за підсумковими даними складений балансовий звіт по народному господарству за
фіксований період часу за формою, наведеною в табл. 1.
,
за підсумковими даними складений балансовий звіт по народному господарству за
фіксований період часу за формою, наведеною в табл. 1.
Таблиця 1
|
Галузі |
1 | 2 | … |
|
|
|
Продукти |
|||||
| 1 |
|
|
… |
|
|
| 2 |
|
|
… |
|
|
| … | … | … | … | … | … |
|
|
|
|
… |
|
|
| Валовий випуск |
|
|
… |
|
|
| Кінцеве споживання |
|
|
… |
|
Величини ![]() вказують обсяг продукту з
номером
вказують обсяг продукту з
номером ![]() , витрачений галуззю
, витрачений галуззю ![]() в процесі виробництва за
звітний період. Числа
в процесі виробництва за
звітний період. Числа ![]() ,
, ![]() дорівнюють обсягу
продукції (валовому випуску)
дорівнюють обсягу
продукції (валовому випуску) ![]() -ї
галузі за той самий період, а значення
-ї
галузі за той самий період, а значення ![]() –
обсягу продукції
–
обсягу продукції ![]() -ї галузі, що був
спожитий у невиробничій сфері. Числа
-ї галузі, що був
спожитий у невиробничій сфері. Числа ![]() ,
,![]() показують розподіл
показують розподіл ![]() -го продукту на виробничі
потреби всіх інших галузей. Балансовий характер табл. 1 виражається в тому, що
мають виконуватися співвідношення
-го продукту на виробничі
потреби всіх інших галузей. Балансовий характер табл. 1 виражається в тому, що
мають виконуватися співвідношення
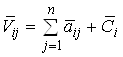 ,
, ![]() .(3)
.(3)
Отже, валова продукція визначається як сума кінцевої й проміжної продукції.
Одиниці виміру всіх зазначених величин можуть бути натуральними або вартісними, залежно від чого розрізняють натуральний і вартісний міжгалузевий баланс.
Якщо всі елементи
![]() -го стовпця таблиці 1
розділити на
-го стовпця таблиці 1
розділити на ![]() , то число
, то число ![]() розумітимемо як обсяг
продукції
розумітимемо як обсяг
продукції ![]() -ї галузі, необхідний для
виробництва однієї одиниці продукту
-ї галузі, необхідний для
виробництва однієї одиниці продукту ![]() -ї
галузі. Числа
-ї
галузі. Числа ![]() ,
, ![]() характеризують технологію
характеризують технологію ![]() -ї галузі у звітний період
і звуться коефіцієнтами прямих витрат
-ї галузі у звітний період
і звуться коефіцієнтами прямих витрат ![]() -ї
галузі. Під
-ї
галузі. Під ![]() розумітимемо частку
продукції
розумітимемо частку
продукції ![]() -ї галузі, витрачену на
невиробниче споживання. Основним елементом схеми міжгалузевого балансу є
квадратна матриця
-ї галузі, витрачену на
невиробниче споживання. Основним елементом схеми міжгалузевого балансу є
квадратна матриця ![]() , яку називають
матрицею коефіцієнтів прямих витрат.
, яку називають
матрицею коефіцієнтів прямих витрат.
Першим
допущенням даної схеми є те, що сформована технологія виробництва є незмінною
протягом деякого проміжку часу. Друге допущення полягає в тому, що для
виробництва ![]() одиниць продукції галузі
одиниць продукції галузі ![]() необхідно затратити
необхідно затратити ![]() одиниць галузі
одиниць галузі ![]() , тобто передбачається, що
витрати прямо пропорційні випуску (є лінійно однорідною функцією випуску).
, тобто передбачається, що
витрати прямо пропорційні випуску (є лінійно однорідною функцією випуску).
Під час
виробництва набору продукції ![]() витрати
продукції
витрати
продукції ![]() -ї галузі складуть у цьому
випадку величину
-ї галузі складуть у цьому
випадку величину
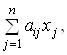
![]() .(4)
.(4)
Переходячи до
матричних позначень, стверджуємо, що вектор виробничих витрат дорівнює ![]() . Якщо
. Якщо ![]() – вектор кінцевих споживань,
тоді валова продукція
– вектор кінцевих споживань,
тоді валова продукція ![]() -ї галузі
дорівнює
-ї галузі
дорівнює
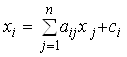 ,
, ![]() (5)
(5)
або в матричній формі
![]() . (6)
. (6)
Систему рівнянь
(6) називають моделлю міжгалузевого балансу або моделлю Леонтьєва. Дана модель
пов'язує обсяги валових випусків з обсягами кінцевої продукції й може бути
використана для розрахунку цих величин. Наприклад, якщо відомий набір можливих
при даних ресурсах випусків ![]() , то
система (6) дозволить розрахувати набір відповідних значень
, то
система (6) дозволить розрахувати набір відповідних значень ![]() . Якщо спочатку відомий
бажаний набір кінцевої продукції, то за допомогою моделі (6) можна визначити
необхідні для його забезпечення обсяги валового випуску по галузі, тобто
. Якщо спочатку відомий
бажаний набір кінцевої продукції, то за допомогою моделі (6) можна визначити
необхідні для його забезпечення обсяги валового випуску по галузі, тобто
![]() (7)
(7)
при заданій
матриці ![]() .
.
3. Розв’язок моделі Леонтьєва
За економічними
міркуваннями всі коефіцієнти матриці ![]() невід’ємні:
невід’ємні:
![]() ,
, ![]() . У цьому випадку говорять,
що матриця
. У цьому випадку говорять,
що матриця ![]() невід’ємна й записують
невід’ємна й записують ![]() . Невід’ємні компоненти
заданого вектора
. Невід’ємні компоненти
заданого вектора ![]() або
або ![]() .
.
Розв’язок, який має бути знайдений, за
змістом також повинний мати тільки невід’ємні компоненти, тобто потрібне виконання нерівностей ![]() або
або ![]() . Можливість одержання
невід’ємного розв’язку визначається властивостями матриці
. Можливість одержання
невід’ємного розв’язку визначається властивостями матриці
![]() .
.
Матриця ![]() називається продуктивною,
якщо існують два вектори
називається продуктивною,
якщо існують два вектори ![]() і
і ![]() , такі, що
, такі, що ![]() .
.
Продуктивність
матриці ![]() означає, що виробнича
система здатна забезпечити деякий позитивний кінцевий випуск за всіма
продуктами.
означає, що виробнича
система здатна забезпечити деякий позитивний кінцевий випуск за всіма
продуктами.
Розглянемо умови
продуктивності матриці ![]() :
:
1) послідовні
головні мінори матриці ![]() позитивні, тобто
для кожного
позитивні, тобто
для кожного ![]() виконана нерівність
виконана нерівність
 ;
;
2) матриця ![]() невід’ємно зворотна, це
означає , що існує зворотна матриця
невід’ємно зворотна, це
означає , що існує зворотна матриця ![]() й всі
її елементи невід’ємні:
й всі
її елементи невід’ємні: ![]()
3) матричний ряд 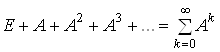 збігається, причому
збігається, причому
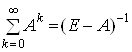 .
.
4) максимальне
власне число ![]() .
.
Повернемося до
системи рівнянь (7). За заданим вектором ![]() потрібно
знайти вектор
потрібно
знайти вектор ![]() , для якого
, для якого ![]() . Перепишемо систему (7) у
вигляді
. Перепишемо систему (7) у
вигляді ![]() , де
, де ![]() – одинична матриця. Якщо
матриця
– одинична матриця. Якщо
матриця ![]() продуктивна, то відповідно
до умови 2) матриця
продуктивна, то відповідно
до умови 2) матриця ![]() існує й невід’ємна. Тому розв’язок системи рівнянь
(7) існує, єдиний і має вигляд
існує й невід’ємна. Тому розв’язок системи рівнянь
(7) існує, єдиний і має вигляд ![]() . Через
те, що
. Через
те, що ![]() й
й ![]() ,
, ![]() .
.
Особливістю
матриці ![]() в моделі Леонтьєва є те,
що всі елементи її невід’ємні. Такі матриці володіють рядом властивостей.
Розглянемо їх в наступному підрозділі.
в моделі Леонтьєва є те,
що всі елементи її невід’ємні. Такі матриці володіють рядом властивостей.
Розглянемо їх в наступному підрозділі.
4. Властивості невід’ємних матриць
Нехай ![]() – квадратна матриця
розміром
– квадратна матриця
розміром ![]() з невід’ємними елементами
з невід’ємними елементами ![]() ,
, ![]() ;
; ![]() підмножина множини
підмножина множини ![]() натуральних чисел
натуральних чисел ![]() . Говорять, що
. Говорять, що ![]() ізольовано (щодо даної
матриці
ізольовано (щодо даної
матриці ![]() ), якщо в матриці
), якщо в матриці ![]()
![]() при
при ![]() ,
, ![]() .
.
Мовою моделі
Леонтьєва ізольованість множини ![]() означає,
що галузі з номерами
означає,
що галузі з номерами ![]() під час свого
функціонування не використовують товари, вироблені галузями з номерами з множин
під час свого
функціонування не використовують товари, вироблені галузями з номерами з множин
![]() . Інакше кажучи, частина
економіки, що утвориться галузями з множини
. Інакше кажучи, частина
економіки, що утвориться галузями з множини ![]() ,
може існувати незалежно від інших галузей. Якщо перенумерувати індекси так, щоб
,
може існувати незалежно від інших галузей. Якщо перенумерувати індекси так, щоб
![]() ,
, ![]() , що відповідає одночасній
перестановці рядків і стовпців матриці
, що відповідає одночасній
перестановці рядків і стовпців матриці ![]() ,
то матриця
,
то матриця ![]() матиме вигляд
матиме вигляд
 ,(8)
,(8)
де ![]() й
й ![]() – квадратні підматриці
розмірів
– квадратні підматриці
розмірів ![]() і
і ![]() відповідно,
відповідно, ![]() –
– ![]() .
.
Матриця ![]() називається нерозкладною,
якщо в множині
називається нерозкладною,
якщо в множині ![]() немає ізольованих
підмножин, крім самої
немає ізольованих
підмножин, крім самої ![]() і порожньої
множини.
і порожньої
множини.
Інакше кажучи,
матриця ![]() нерозкладна, якщо
одночасною перестановкою рядків і стовпців її не можна привести до вигляду (8).
нерозкладна, якщо
одночасною перестановкою рядків і стовпців її не можна привести до вигляду (8).
Нерозкладність
матриці ![]() в моделі Леонтьєва
означає, що кожна галузь використовує хоча й побічно, продукцію всіх галузей.
в моделі Леонтьєва
означає, що кожна галузь використовує хоча й побічно, продукцію всіх галузей.
Розглянемо деякі властивості нерозкладних матриць:
1. Нерозкладна
матриця не має нульових рядків і стовпців; якщо ![]() -й
рядок матриці
-й
рядок матриці ![]() нульовий, то
множина
нульовий, то
множина ![]() ізольована.
ізольована.
2. Якщо ![]() – нерозкладна й
– нерозкладна й ![]() то
то ![]() .
.
Теорема
Фробеніуса-Перрона: нерозкладна матриця ![]() має
таке власне число
має
таке власне число ![]() , що й модулі
всіх інших власних чисел матриці
, що й модулі
всіх інших власних чисел матриці ![]() не
перевищують
не
перевищують ![]() ; числу
; числу ![]() відповідає з точністю до
скалярного множника власний вектор
відповідає з точністю до
скалярного множника власний вектор ![]() , всі
координати якого ненульові й одного знака, тобто можна вважати
, всі
координати якого ненульові й одного знака, тобто можна вважати ![]() .
.
4. Лема: нехай ![]() – нерозкладна матриця,
– нерозкладна матриця, ![]() ,
, ![]() ,
, ![]() , крім того, у вектора
, крім того, у вектора ![]() є нульові координати та
є нульові координати та ![]() , тоді у вектора
, тоді у вектора ![]() знайдеться додатна
координата
знайдеться додатна
координата ![]() , причому
, причому ![]() .
.
5. Лема: якщо
матриця ![]() нерозкладна,
нерозкладна, ![]() ,
, ![]() , то з нерівності
, то з нерівності ![]() випливає, що
випливає, що ![]() ,
, ![]() .
.
5. Зв'язок між коефіцієнтами прямих і повних витрат
Нехай
розглядається матриця коефіцієнтів прямих витрат у натуральному або вартісному
виразі ![]() .
.
Для виробництва
одиниці продукції ![]() -ї галузі
необхідно затратити набір продуктів
-ї галузі
необхідно затратити набір продуктів ![]() , що
описується
, що
описується ![]() -м стовпцем матриці
-м стовпцем матриці ![]() . Але для виробництва цього
набору
. Але для виробництва цього
набору ![]() необхідно безпосередньо
затратити набір продуктів, який ми позначимо через
необхідно безпосередньо
затратити набір продуктів, який ми позначимо через ![]() .
.
Елементи вектора
витрат ![]() називаються коефіцієнтами
непрямих витрат першого порядку відповідних продуктів на виробництво одиниць
називаються коефіцієнтами
непрямих витрат першого порядку відповідних продуктів на виробництво одиниць ![]() -го продукту
-го продукту ![]() .
.
Матриця ![]() , складена зі стовпців
, складена зі стовпців ![]() ,
, ![]() , називається матрицею
непрямих витрат першого порядку й визначається відповідно до формули
, називається матрицею
непрямих витрат першого порядку й визначається відповідно до формули
![]() .
.
Непрямими
витратами другого порядку називають прямі витрати, необхідні для забезпечення непрямих
витрат першого порядку, тобто ![]() , або в
матричній формі
, або в
матричній формі
![]()
де ![]() – матриця коефіцієнтів
непрямих витрат другого порядку.
– матриця коефіцієнтів
непрямих витрат другого порядку.
Продовжуючи за
аналогією, назвемо непрямими витратами порядку ![]() прямі
витрати на забезпечення непрямих витрат порядку
прямі
витрати на забезпечення непрямих витрат порядку ![]() .
Очевидно, що матрицю коефіцієнтів непрямих витрат
.
Очевидно, що матрицю коефіцієнтів непрямих витрат ![]() -го
порядку одержимо, помноживши
-го
порядку одержимо, помноживши ![]() на
на ![]()
![]() . (9)
. (9)
Визначимо тепер повні
витрати як суму прямих і непрямих витрат усіх порядків. Відповідно до цього
матриця ![]() , складена з коефіцієнтів повних
витрат, утвориться як сума
, складена з коефіцієнтів повних
витрат, утвориться як сума
![]() (10)
(10)
або з огляду на
те, що ![]() , маємо
, маємо
![]() (11)
(11)
Коефіцієнти прямих і повних матеріальних витрат мають важливе значення для характеристики структури техніко-економічних зв'язків і для аналізу ефективності виробництва з боку витрат упредметненої праці. Суттєва відмінність коефіцієнтів повних витрат від коефіцієнтів прямих витрат полягає в тому, що вони є не галузевими, а народногосподарськими показниками й формуються з урахуванням технологічних зв'язків між галузями.
З'ясуємо такий момент. Чи не виявляться будь-які з коефіцієнтів повних витрат нескінченно великими?
Розглянемо
матрицю ![]()
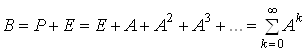 .
.
Очевидно, що
елементи матриці ![]() скінченні разом
з елементами матриці
скінченні разом
з елементами матриці ![]() тільки в тому
випадку, якщо скінченна сума ряду
тільки в тому
випадку, якщо скінченна сума ряду ![]() . Крім
того, відповідно до умови (3) його збіжність є умовою, еквівалентною продуктивності
матриці
. Крім
того, відповідно до умови (3) його збіжність є умовою, еквівалентною продуктивності
матриці ![]() , причому
, причому 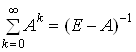 . Отже, у випадку
продуктивності матриці
. Отже, у випадку
продуктивності матриці ![]() й тільки в цьому
випадку матриця повних витрат
й тільки в цьому
випадку матриця повних витрат ![]() скінченна,
її визначають відповідно до формули
скінченна,
її визначають відповідно до формули
![]() .
.
Для великих
значень ![]() важко обчислити зворотну
матрицю. В цьому випадку матрицю
важко обчислити зворотну
матрицю. В цьому випадку матрицю ![]() , як і
матрицю
, як і
матрицю ![]() , можна обчислити
приблизно, користуючись методом ітерацій. На першій ітерації
, можна обчислити
приблизно, користуючись методом ітерацій. На першій ітерації ![]() , на другій ітерації
, на другій ітерації ![]() , на третій
, на третій ![]() , на
, на ![]() -й ітерації
-й ітерації ![]() . Часткова сума
. Часткова сума ![]() відрізняється від
часткової суми
відрізняється від
часткової суми ![]() на величину
на величину ![]() . Через те що ряд
збігається,
. Через те що ряд
збігається, ![]() при
при ![]() . Тому за скінченну
кількість кроків можна досягти заданої точності обчислень.
. Тому за скінченну
кількість кроків можна досягти заданої точності обчислень.
Коефіцієнти ![]() матриці
матриці ![]() мають таку економічну
інтерпретацію: якщо випуск кінцевого
мають таку економічну
інтерпретацію: якщо випуск кінцевого ![]() -го
продукту потрібно збільшити на одиницю, то валовий випуск
-го
продукту потрібно збільшити на одиницю, то валовий випуск ![]() -го продукту має бути
збільшений на
-го продукту має бути
збільшений на ![]() .
.
6. Коефіцієнти трудових витрат. Баланс трудових ресурсів
Модель Леонтьєва, як відзначалося раніше, відображає лише потенційні можливості, закладені в технології виробничого сектора. У даній моделі передбачається, що процес виробництва відбувається миттєво – всі проміжні продукти вважаються виробленими до того моменту, коли в них з'являється потреба, тобто кожна галузь здатна зробити будь-який обсяг своєї продукції за умови, що їй буде забезпечена сировина в необхідній кількості. Насправді, це не так, оскільки виробничі можливості будь-якої галузі обмежені наявним обсягом основних фондів трудових ресурсів.
Розглянемо проблему розподілу трудових ресурсів, яку можна дослідити за допомогою моделі Леонтьєва.
Зіставимо кожній ![]() -ї галузі число
-ї галузі число ![]() , що виражає необхідні витрати
трудових ресурсів при одиничній інтенсивності даного технологічного процесу.
, що виражає необхідні витрати
трудових ресурсів при одиничній інтенсивності даного технологічного процесу.
Нехай ![]() – вектор прямих витрат
праці й
– вектор прямих витрат
праці й ![]() – матриця прямих
матеріальних витрат. На виробництво одиниці продукту виду
– матриця прямих
матеріальних витрат. На виробництво одиниці продукту виду ![]() необхідно безпосередньо
затратити набір продуктів
необхідно безпосередньо
затратити набір продуктів ![]() і
працю в кількості
і
працю в кількості ![]() . Однак на
виробництво даного набору продуктів у свою чергу необхідно затратити
. Однак на
виробництво даного набору продуктів у свою чергу необхідно затратити 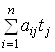 одиниць праці. Ця величина
називається непрямими витратами праці першого порядку на одиницю
одиниць праці. Ця величина
називається непрямими витратами праці першого порядку на одиницю ![]() -го продукту й позначається
через
-го продукту й позначається
через 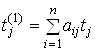 .
.
Вектор непрямих
витрат праці першого порядку ![]() визначається
таким виразом:
визначається
таким виразом: ![]() .
.
Міркуючи
аналогічно тому, як це робилося під час побудови коефіцієнтів непрямих
матеріальних витрат, дійдемо висновку, що вектор ![]() непрямих
витрат праці порядку
непрямих
витрат праці порядку ![]() визначається
таким співвідношенням:
визначається
таким співвідношенням:
![]() або
або ![]() .
.
Повні витрати
праці ![]() є сумою прямих і непрямих
витрат праці
є сумою прямих і непрямих
витрат праці
![]() .
.
У матричному
записі, вважаючи, що ![]() і, з огляду на
те, що
і, з огляду на
те, що ![]() , маємо
, маємо
![]() або
або ![]() .
.
Якщо матриця ![]() продуктивна, то суму в
дужках можна замінити на
продуктивна, то суму в
дужках можна замінити на ![]() й,
отже,
й,
отже, ![]() – матриця повних витрат
праці.
– матриця повних витрат
праці.
Зменшення повних витрат праці на одиницю продукції є узагальнюючим показником збільшення продуктивності праці, ефективності виробництва. Розрахунок коефіцієнтів повних витрат праці важливий для ціноутворення на етапі встановлення об'єктивної основи ціни – вартості. Для обчислення коефіцієнтів повних витрат праці використовують ітераційну процедуру
![]() ,
,
що дозволяє з заданою точністю визначити дані коефіцієнти.