
Главная
Рефераты по зарубежной литературе
Рефераты по логике
Рефераты по маркетингу
Рефераты по международному публичному праву
Рефераты по международному частному праву
Рефераты по международным отношениям
Рефераты по культуре и искусству
Рефераты по менеджменту
Рефераты по металлургии
Рефераты по муниципальному праву
Рефераты по налогообложению
Рефераты по оккультизму и уфологии
Рефераты по педагогике
Рефераты по политологии
Рефераты по праву
Биографии
Рефераты по предпринимательству
Рефераты по психологии
Рефераты по радиоэлектронике
Рефераты по риторике
Рефераты по социологии
Рефераты по статистике
Рефераты по страхованию
Рефераты по строительству
Рефераты по схемотехнике
Рефераты по таможенной системе
Сочинения по литературе и русскому языку
Рефераты по теории государства и права
Рефераты по теории организации
Рефераты по теплотехнике
Рефераты по технологии
Рефераты по товароведению
Рефераты по транспорту
Рефераты по трудовому праву
Рефераты по туризму
Рефераты по уголовному праву и процессу
Рефераты по управлению
Контрольная работа: Экономико-математическое моделирование
Контрольная работа: Экономико-математическое моделирование
1. Определить нижнюю и верхнюю цену игры, заданной платежной матрицей
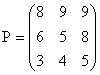
Имеет ли игра седловую точку?
Решение:
Найдем по каждой строчке платежной матрицы минимальное число αi = min (αi1, αi2, αi3) – это гарантированный выигрыш игрока А, при выборе им соответствующей стратегии. Чтобы получить максимально возможный гарантированный выигрыш, игрок А должен выбрать ту стратегию, для которой αij имеет максимальное значение – α = max(α1, α2, α3) – это нижняя цена игры.
Для игрока В выберем по каждому столбцу максимальное число βj = max(α1j, α2j, α3j) – это гарантированный проигрыш игрока В при выборе им стратегии Вj. Найдем минимальное из этих чисел β = min (β 1, β 2, β 3) – это верхняя цена игры. Занесем полученные данные в таблицу 1.
Нижняя цена игры α = 8 равна верхней цене игры β = 8. Значит, игра имеет седловую точку. Для игрока А оптимальная стратегия – А1, для игрока В оптимальная стратегия – В1.
Ответ: α = β = 8, игра имеет седловую точку, оптимальные стратегии (А1, В1).
Таблица 1 – Определение цены игры платежной матрицы
|
В1 |
В2 |
В3 |
||
|
А1 |
8 | 9 | 9 |
α1 = min (8, 9, 9) = 8 |
|
А2 |
6 | 5 | 8 |
α2 = min (6, 5, 8) = 5 |
|
А3 |
3 | 4 | 5 |
α3 = min (3, 4, 5) = 3 |
|
β1 = max(8, 6, 3) β1= 8 |
β2 = max(9, 5, 4) β2= 9 |
β3 = max(9, 8, 5) β3= 9 |
α = max(8, 5, 3) = 8 β = min (8, 9, 9) = 8 |
2. Решить графически игру, заданную платежной матрицей
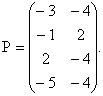
Решение:
Дана игра 4 х 2 , то есть у игрока А имеется 4 стратегии, а у игрока В – 2. Поэтому, будем решать игру для игрока В. Построим оси: ОХ – на ней будем отмечать вероятности, с которыми игрок использует ту или иную стратегии, и ОУ – на ней будем откладывать цену игры. На расстоянии единица от оси ОУ проведем еще ось параллельную ей, как показано на рисунке 1.
Если игрок А выбирает стратегию А1, то игрок В, используя свои стратегии с вероятностями (q1, q2), будет проигрывать, в среднем, q1∙α11+q2∙α12 = q1∙(-3) +q2∙(-4). Отметим на оси ОУ α11 = -3, а на оси ей параллельной α12 = -4 и соединим эти точки прямой линией – она показывает, сколько, в среднем, получает игрок В, если А использует стратегию А1, а В чередует стратегии В1 и В2 с некоторыми вероятностями (q1, q2). Аналогично отмечаем на оси ОУ точку -1, а на параллельной ей оси – точку 2 и соединяем отрезком. Получаем линию, показывающую, сколько, в среднем, получает игрок В, если А выбрал стратегию А2. Точно также для А3 и А4.
Для игрока В надо выбрать верхнюю границу, так как он должен рассчитывать, что А выберет ту стратегию, которая соответствует наибольшему проигрышу для игрока В. На рисунке 1 это ломанная А3КА2, выделенная толстой линией. Игроку В следует выбрать ту смешанную стратегию, которая соответствует наименьшему проигрышу для В – точка К. Это точка пересечения прямых, соответствующих стратегиям А3 и А2. Выпишем уравнения этих прямых.
Прямая (А3 А3) проходит через точки с координатами (0;2) и (1;-4). Уравнение этой прямой запишется в следующем виде:
![]()
Уравнение прямой (А2 А2), проходящей через точки (0;-1) и (1;2), запишется в следующем виде:
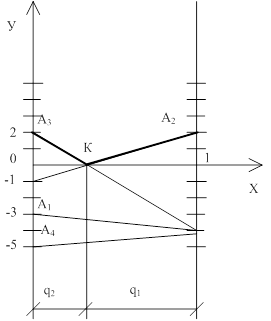
Рисунок 1 –Графическое решение
![]()
Точка К – точка пересечения этих прямых, имеет координаты, удовлетворяющие системе:
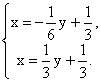
Решение системы: ![]()
Следовательно, цена игры ν = 0, оптимальная стратегия для игрока В:
![]()
Для игрока А, стратегии А1 и А4 будут не активными, игроку А не выгодно их использовать. Максимально возможный выигрыш, равный цене игры ν = 0, игрок А будет получать, используя стратегии А2 и А3. Найдем оптимальную смешанную стратегию для игрока А из следующей системы, учитывая, что А1 и А4 не активные стратегии, то есть р1 = р4 = 0:
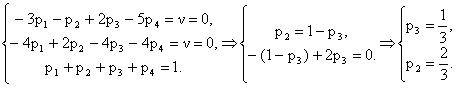
Ответ: Цена игры ν = 0, оптимальные
стратегии игроков ![]()
3. Решить геометрически следующую задачу линейного программирования:
![]() при ограничениях:
при ограничениях: 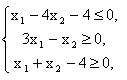
![]()
Решение:
Построим область
ограничений. Строим прямую (1): x1 – 4x2 - 4 = 0 по двум точкам, координаты которых удовлетворяют
уравнению: (8; 1), (4; 0), как показано на рисунке 2. Проверяем, какая
полуплоскость удовлетворяет неравенству ![]() ,
для этого подставим значение произвольной точки (0; 0) в это неравенство,
получим
,
для этого подставим значение произвольной точки (0; 0) в это неравенство,
получим ![]() - выполняется. Аналогичным
способом строим прямые (2):
- выполняется. Аналогичным
способом строим прямые (2): ![]() и (3):
и (3): ![]() , выделяем «бородой»
области значений x1, x2, удовлетворяющие условиям
, выделяем «бородой»
области значений x1, x2, удовлетворяющие условиям ![]() и
и
![]() . На рисунке 2 изображена
область, удовлетворяющая представленной в условиях задачи системе. Заметим, что
. На рисунке 2 изображена
область, удовлетворяющая представленной в условиях задачи системе. Заметим, что
![]() и одно из неравенств
системы -
и одно из неравенств
системы - ![]() , тогда, очевидно, функция F принимает значения интервала
, тогда, очевидно, функция F принимает значения интервала ![]() , но
, но ![]() , тогда Fmax =
, тогда Fmax = ![]() .
.
Ответ: Fmax = ![]() .
.
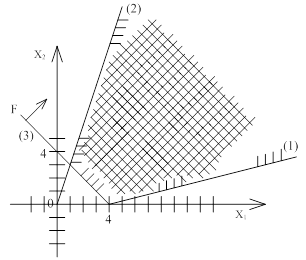
Рисунок 2 – Графическое решение
4. Для выпуска двух видов продукции А и В предприятие использует 4 вида ресурсов, все данные представлены в следующей таблице:
| Вид ресурса | Расход ресурсов для выпуска одного изделия | Наличие ресурса | |
| А | В | ||
| Рабочая сила | 1 | 3 | 3 |
| Сырье | 6 | 3 | 24 |
| Оборудование | 2 | 5 | 20 |
| Производственные ресурсы | 2 | 2 | 10 |
Прибыль от реализации единицы продукции А и В составляет 50 и 70 ДЕ, соответственно. Предприятие может нанять людей на работу, а увольнять людей не разрешается. Составить план выпуска продукции, чтобы прибыль от ее реализации была максимальной. Сколько человек придется нанять?
Решение:
Обозначим x1, x2 – число единиц продукции соответственно А и В, запланированных к производству. По условию для их изготовления потребуется (1∙ x1 + 3∙ x2) единиц ресурса «Рабочая сила», (6∙ x1 + 3∙ x2) единиц ресурса «Сырье», (2∙ x1 + 5∙ x2) единиц ресурса «Оборудование», (2∙ x1 + 2∙ x2) единиц ресурса «Производственные ресурсы». Так как потребление всех этих видов ресурсов не должно превышать наличие ресурсов, то связь между потреблением ресурсов и их запасами выразится системой неравенств:
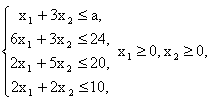
где а ≥ 3 и а – целое число (количество работников).
Суммарная прибыль стремиться к максимальному значению:
![]()
Все значения x1 и x2 лежат в I четверти, а функция F – луч, исходящий из точки (0; 0) под углом α к оси ОX1, где ![]() т.е.
т.е. ![]() - функция прибыли F. Строим графическое решение для
неравенств (2):
- функция прибыли F. Строим графическое решение для
неравенств (2): ![]() , (3):
, (3): ![]() , (4):
, (4): ![]() , как это показано на
рисунке 3.
, как это показано на
рисунке 3.
Максимально возможная
прибыль из графического решения в точке К, координаты которой находим из
системы: 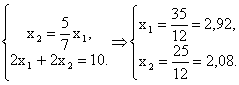
С учетом, x1, x2 – целые числа (только конечный
продукт можно продать и получить прибыль), находим: при х1 = х2
= 2 возможно получение максимальной прибыли ![]() Подставив
х1 = х2 = 2 в неравенство (1):
Подставив
х1 = х2 = 2 в неравенство (1): ![]() , получим
, получим ![]() ,т.е. а = 8. Необходимо
дополнительно нанять 8 – 3 = 5 человек.
,т.е. а = 8. Необходимо
дополнительно нанять 8 – 3 = 5 человек.
Ответ: Максимально возможная прибыль 240 ДЕ возможна при производстве изделий А – 2шт. и изделий В – 2 шт., при этом придется дополнительно нанять 5 работников.
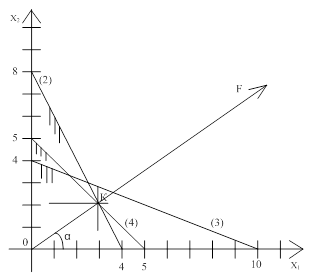
Рисунок 3 – Графическое решение
5. Построить граф состояний следующего случайного процесса: система состоит из двух аппаратов по продаже билетов, каждый из которых в случайный момент времени может быть либо занятым, либо свободным.
Решение:
Система может находиться в четырех состояниях, так как у каждого аппарата по продаже билетов есть два состояния (быть занятым или свободным). Пусть S0 – оба аппарата заняты; S1 – 1-ый занят, 2-ой свободен; S2 – 1-ый свободен, 2-ой занят; S3 – оба аппарата свободны. Построим граф состояний, отметив на нем все возможные состояния кругами, а возможные переходы из состояния в состояние обозначим стрелками. Получаем, что переход из S0 в S3 возможен либо через S1, либо через S2, либо напрямик, как показано на рисунке 4.
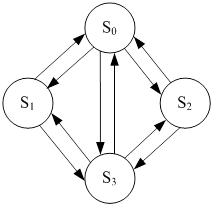
Рисунок 4 – Граф состояний аппаратов по продаже билетов
6. Найти предельные вероятности для системы S, граф которой изображен на рисунке.
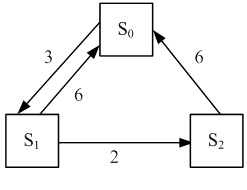
Решение:
В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют. Их можно найти из уравнений Колмогорова, составив систему по данному размеченному графу состояний, по следующему правилу:
Слева в уравнении стоит предельная вероятность данного состояния pi, умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа – сумма произведений интенсивностей всех потоков, входящих в данное состояние, на вероятности тех состояний, из которых эти состояния выходят.
Кроме этого надо
учитывать, что сумма всех вероятностей данной конечной системы равна единице.
Составим уравнения для состояний S1 и S2 (уравнение для состояния S0 – «лишнее»): 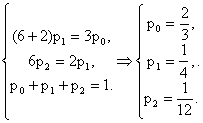
Ответ: Система примерно 66,67% времени пребывает в состоянии S0, 25% - в состоянии S1 и 8,33% времени находится в состоянии S2.
7. Найти валовой выпуск для сбалансированной многоотраслевой экономики в модели Леонтьева, если дана матрица прямых затрат А и вектор конечного потребления У:
![]()
Решение:
Для сбалансированной многоотраслевой экономики выполняется следующее соотношение:
![]()
| где | Х | - | вектор валового выпуска; |
| У | - | вектор конечного потребления; | |
| А | - | матрица прямых затрат. |
Выразим валовой выпуск через конечное потребление и матрицу затрат:
![]()
Находим матрицу, обратную к (Е – А):
![]()
![]()
![]()
Найдем валовой выпуск:
Х = ![]()
Ответ: Валовой выпуск равен (811,3; 660,4).
*При решении задач использовался источник:
Алесинская Т.В. Учебное пособие по решению задач по курсу "Экономико-математические методы и модели". - Таганрог: Изд-во ТРТУ, 2002. - 153 с.